Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 18 SGK Toán 8 – Cánh diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Biểu đồ hình quạt tròn ở Hình 28
Đề bài
Biểu đồ hình quạt tròn ở Hình 28 biểu diễn tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của một trường đại học về những lớp động vật có xương sống: Cá, Lưỡng cư; Bò sát; Chim; Động vật có vú.
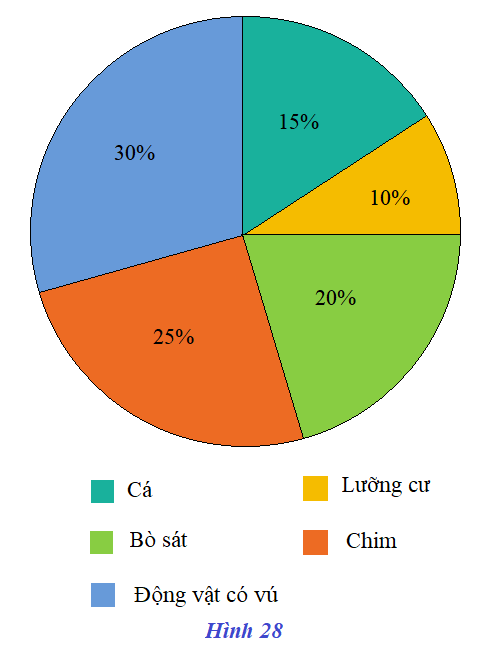
Lập bảng thống kê tỉ lệ các loại mẫu vật đó trong bảo tàng sinh vật theo mẫu sau:
Lớp động vật có xương sống | Cá | Lưỡng cư | Bò sát | Chim | Động vật có vú |
Tỉ lệ mẫu vật (%) | ? | ? | ? | ? | ? |
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào các số liệu cho ở biểu đồ quạt tròn, điền tỉ lệ mẫu vật vào các ô tương ứng với các lớp động vật.
Lời giải chi tiết
Dựa vào biểu đồ quạt tròn, ta có bảng thống kê sau:
Lớp động vật có xương sống | Cá | Lưỡng cư | Bò sát | Chim | Động vật có vú |
Tỉ lệ mẫu vật (%) | 15 | 10 | 20 | 25 | 30 |
Bài 5 trang 18 SGK Toán 8 – Cánh diều thuộc chương trình đại số, tập trung vào việc thực hành các phép toán với đa thức. Cụ thể, bài tập yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia đa thức, đồng thời áp dụng các quy tắc về dấu và bậc của đa thức.
Bài 5 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải câu a), ta cần thực hiện phép cộng hai đa thức. Lưu ý rằng chỉ có các hạng tử đồng dạng mới được cộng với nhau. Ví dụ, nếu có hai đa thức A = 2x2 + 3x - 1 và B = -x2 + 5x + 2, thì A + B = (2x2 - x2) + (3x + 5x) + (-1 + 2) = x2 + 8x + 1.
Câu b) yêu cầu thực hiện phép trừ hai đa thức. Tương tự như phép cộng, ta chỉ trừ các hạng tử đồng dạng với nhau. Ví dụ, nếu A = 3x3 - 2x2 + x và B = x3 + x2 - 3x, thì A - B = (3x3 - x3) + (-2x2 - x2) + (x + 3x) = 2x3 - 3x2 + 4x.
Câu c) yêu cầu thực hiện phép nhân hai đa thức. Để nhân hai đa thức, ta nhân mỗi hạng tử của đa thức thứ nhất với mỗi hạng tử của đa thức thứ hai, sau đó cộng các kết quả lại với nhau. Ví dụ, nếu A = x + 2 và B = x - 3, thì A * B = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6.
Câu d) yêu cầu thực hiện phép chia hai đa thức. Phép chia đa thức có thể được thực hiện bằng phương pháp chia trực tiếp hoặc sử dụng sơ đồ Horner. Phương pháp chia trực tiếp thường được sử dụng khi chia đa thức bậc cao cho đa thức bậc thấp. Sơ đồ Horner thường được sử dụng khi chia đa thức cho đa thức bậc nhất.
Giả sử ta có đa thức P(x) = 2x2 - 5x + 3. Để kiểm tra xem x = 1 có phải là nghiệm của đa thức P(x) hay không, ta thay x = 1 vào đa thức và tính giá trị của P(1). Nếu P(1) = 0, thì x = 1 là nghiệm của đa thức P(x). Trong trường hợp này, P(1) = 2(1)2 - 5(1) + 3 = 2 - 5 + 3 = 0. Vậy x = 1 là nghiệm của đa thức P(x).
Việc giải bài tập về đa thức có nhiều ứng dụng trong thực tế, bao gồm:
Bài 5 trang 18 SGK Toán 8 – Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với đa thức. Hy vọng rằng với hướng dẫn chi tiết này, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.