Chào mừng bạn đến với bài học lý thuyết Hình chóp tứ giác đều trong chương trình Toán 8 Cánh diều. Bài viết này sẽ cung cấp đầy đủ kiến thức cơ bản, định nghĩa, tính chất và các ví dụ minh họa để bạn hiểu rõ về hình chóp tứ giác đều.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán, giúp bạn học tập hiệu quả và đạt kết quả cao.
Hình chóp tứ giác đều
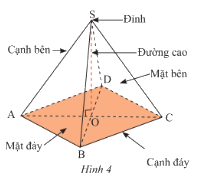
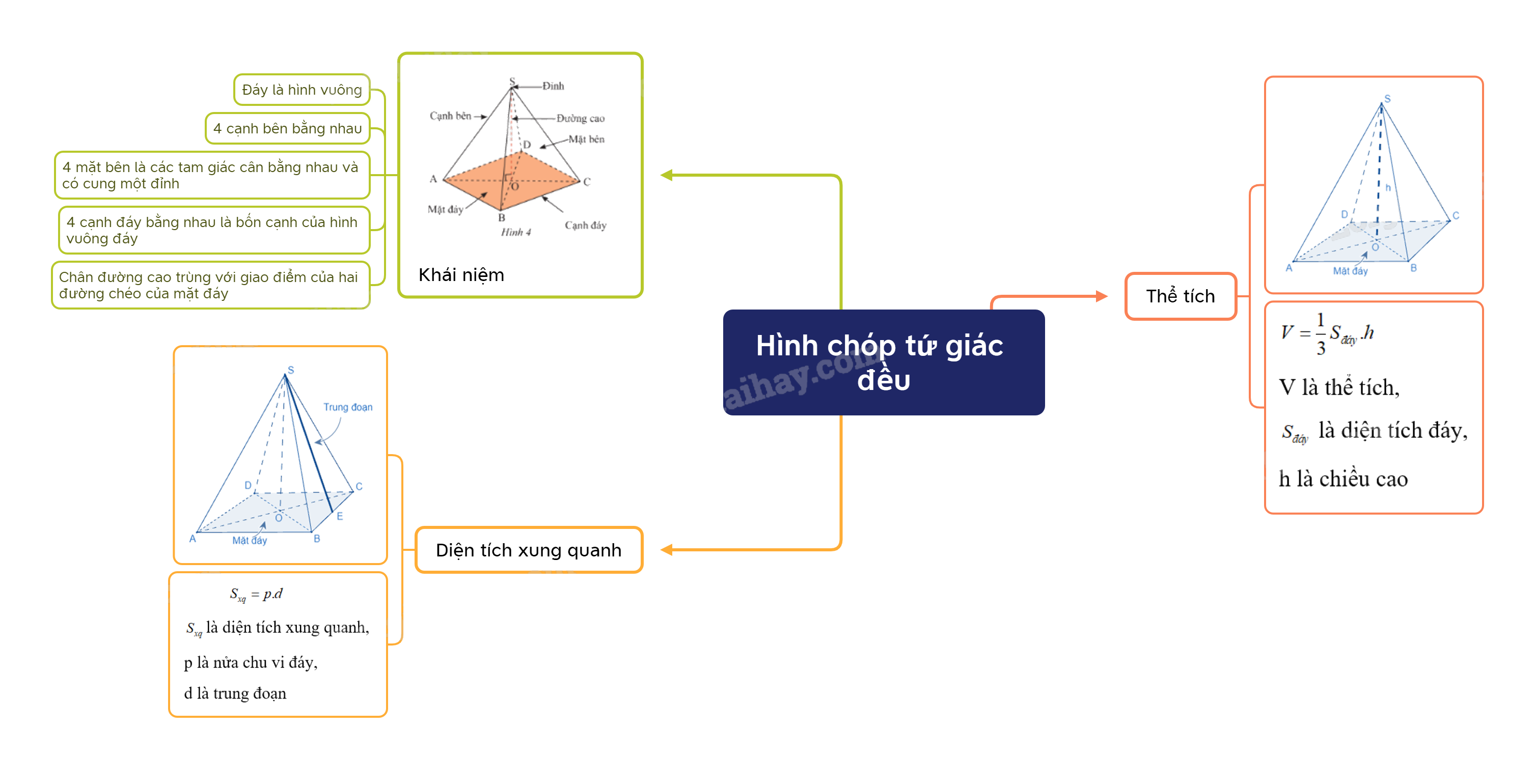
Hình chóp tứ giác đều có:
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy.
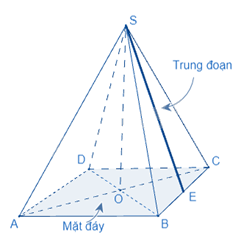
Diện tích xung quanh của hình chóp tam giác đều bằng nửa chu vi đáy với độ dài trung đoạn.
\(S_{xq}=p.d\)
(\(S_{xq}\) là diện tích xung quanh, p là nửa chu vi đáy, d là trung đoạn)
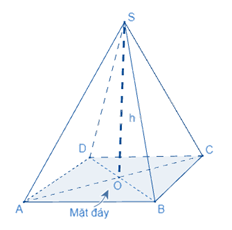
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng \(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(V = \frac{1}{3}{S_{đáy}}.h\)
(V là thể tích, \({S_{đáy}}\) là diện tích đáy, h là chiều cao)
Ví dụ:
Cho hình chóp tứ giác đều sau:
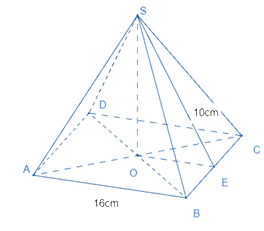
Thể tích của hình chóp là: \(V = \frac{1}{3}.6.16.16 = 512(c{m^3})\)
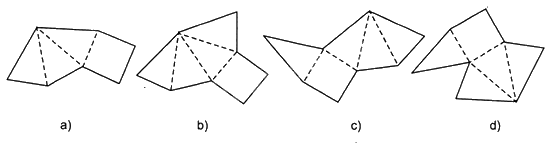
Câu 1. Trong các tấm bìa bên dưới, có mấy hình gấp lại được thành hình chóp tứ giác đều
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải
Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.
Đáp án: B
Câu 2. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, nếu tăng cạnh bên lên hai lần thì chu vi mặt đáy sẽ:
A. Giảm đi 2 lần
B. Tăng lên 2 lần
C. Giảm đi 4 lần.
D. Tăng lên 4 lần.
Lời giải
Hình chóp tứ giác đều có đáy là hình vuông, tất cả các cạnh đều bằng nhau nên cạnh bên tăng lên hai lần thì cạnh đáy tăng hai lần. Khi đó chu vi hình vuông cũng tăng lên 2 lần.
Đáp án: B
Câu 3. Chọn câu trả lời đúng: Hình chóp tứ giác đều có:
A. 4 cạnh, 1 đỉnh, 4 mặt
B. 8 cạnh, 1 đỉnh, 5 mặt
C. 6 cạnh, 1 đỉnh, 4 mặt
D. 8 cạnh, 4 đỉnh, 5 mặt
Lời giải
Hình chóp tứ giác đều có 1 đỉnh, 8 cạnh và 5 mặt.
Đáp án: B
Câu 4. Tính diện tích xung quanh của hình chóp tứ giác đều biết chiều cao một mặt bên của hình chóp bằng 5cm, cạnh đáy của hình chóp bằng 4cm.
A. \(20c{m^2}\).
B. \(60c{m^2}\).
C. \(40c{m^2}\)
D. \(80c{m^2}\)
Lời giải
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên mà hình chóp tứ giác đều có 4 mặt bên nên \({S_{xq}} = S.4 = (\frac{1}{2}.5.4).4 = 40c{m^2}\) nên chọn đáp án C.
Đáp án: C
Câu 5. Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của hình chóp là \(9cm\). Tính thể tích của hình chóp đó.
Lời giải
Theo công thức thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h = \frac{1}{3}.(4.4).9 = 48c{m^3}\)
Câu 6. Cho khối chóp tứ giác đều, nếu tăng cạnh đáy lên ba lần và giảm chiều cao đi ba lần thì thể tích của khối chóp sẽ:
A. Giảm đi 9 lần.
B. Tăng lên 3 lần.
C. Giảm đi 3 lần.
D. Tăng lên 9 lần.
Lời giải
Nếu cạnh đáy tăng lên 3 lần thì diện tích đáy tăng 9 lần. Vì chiều cao giảm đi 3 lần nên thể tích khối chóp tăng lên 3 lần.
Đáp án: B
Câu 7. Một hình chóp tứ giác đều có thể tích bằng \(50c{m^3}\), chiều cao hình chóp bằng 6cm, chiều cao mặt bên bằng 4cm. Tính diện tích xung quanh hình chóp đó.
Lời giải
Diện tích đáy của hình chóp là : \(50.3:6 = 25c{m^2}\)
Gọi x là độ dài cạnh đáy, vì đáy hình chóp tứ giác đều là hình vuông nên ta có
\({x^2} = 25 \Rightarrow x = 5cm\).
Diện tích một mặt bên là: \(S = \frac{1}{2}.5.4 = 10(c{m^2})\)
Diện tích xung quanh của hình chóp trên là: \({S_{xq}} = 4.S = 4.10 = 40(c{m^2})\)
Câu 8. Cho hình chóp tứ giác đều S. ABCD có diện tích xung quanh bằng \(72c{m^2}\) , chiều cao có độ dài bằng 6cm, chiều cao một mặt bên là 4cm .Thể tích của khối chóp đó là?
Lời giải
Diện tích một mặt bên là: \(72:4 = 18c{m^2}\)
Độ dài cạnh đáy là: \(18.2:4 = 9cm\)
Diện tích mặt đáy là: \({S_{ABCD}} = 9.9 = 81c{m^2}\)
Áp dụng công thức thể tích khối chóp ta được: \(V = \frac{1}{3}.81.6 = 162c{m^3}\)
Câu 9. Một cái bể hình hộp chữ nhật đựng nước, có chiều dài 1,2m; chiều rộng 0,9m, chiều cao 1m. Hiện tại mực nước trong bể cao 0,5m. Người ta dùng 1 chiếc gầu hình chóp tam giác đều diện tích đáy \(1800c{m^2}\), chiều cao 20cm để múc nước vào bể. Cần múc bao nhiêu lần để đầy nước trong bể? (mỗi lần múc đầy gầu)
Lời giải
Thể tích nước cần để đổ vào bể là:
\({V_{nuoc}} = 1,2.0,9.(1 - 0,5) = 0,54({m^3}) = 540\)(lít)
Thể tích gầu nước là:
\({V_{gau}} = \frac{1}{3}.1800.20 = 12000(c{m^3}) = 12\)(lít)
Số lần cần múc để hết nước trong bể là: \(540:12 = 45\)(lần)
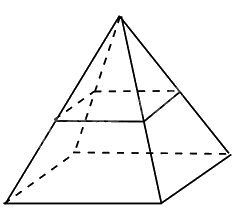
Câu 10. Người ta làm một bugalow dạng hình chóp tứ giác đều có chiều cao 4m, cạnh sàn nhà bằng 6m. Người ta chia đôi làm hai tầng bằng một mặt phẳng song song với sàn, cách đỉnh của hình chóp một khoảng bằng nửa chiều cao, cạnh mặt sàn tầng hai bằng một nửa cạnh mặt sàn tầng một. Biết một người cần \(3{m^3}\)không khí, tính số người tối đa ở tầng dưới. ( hình vẽ dưới)
Lời giải
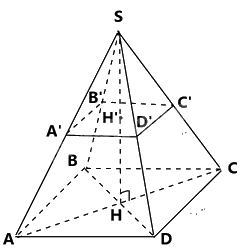
\(SH = 4m\)là chiều cao của bugalow
\( \Rightarrow SH' = \frac{{SH}}{2} = 2m\)
\(A'B' = \frac{1}{2}.AB = \frac{1}{2}.6 = 3m\)
Ta có:
\(\begin{array}{l}{S_{A'B'C'D'}} = 3.3 = 9{m^2}\\{S_{ABCD}} = 6.6 = 36{m^2}\end{array}\)
\(\begin{array}{l}{V_{S.A'B'C'D'}} = \frac{1}{3}.{S_{A'B'C'D'}}.SH' = \frac{1}{3}.9.2 = 6{m^3}\\{V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SH = \frac{1}{3}.36.4 = 48{m^3}\end{array}\)
Thể tích phần không gian còn lại ở tầng dưới là: \(V = {V_{S.ABCD}} - {V_{S.A'B'C'D'}} = 48 - 6 = 42{m^3}\)
Hình chóp tứ giác đều là một trong những hình khối quan trọng trong chương trình Hình học không gian lớp 8. Việc nắm vững lý thuyết về hình chóp tứ giác đều là nền tảng để giải quyết các bài tập liên quan và hiểu sâu hơn về các khái niệm hình học khác.
Hình chóp tứ giác đều là hình chóp có đáy là một tứ giác đều và đỉnh của hình chóp nằm trên đường thẳng vuông góc với tâm của đáy.
Một hình chóp tứ giác đều có các yếu tố sau:
Hình chóp tứ giác đều có những tính chất quan trọng sau:
Diện tích xung quanh của hình chóp tứ giác đều được tính bằng công thức:
Sxq = p * d
Trong đó:
Diện tích toàn phần của hình chóp tứ giác đều được tính bằng công thức:
Stp = Sxq + Sđáy
Trong đó:
Thể tích của hình chóp tứ giác đều được tính bằng công thức:
V = (1/3) * Sđáy * h
Trong đó:
Bài tập 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 5cm và chiều cao SH = 4cm. Tính diện tích xung quanh và thể tích của hình chóp.
Giải:
Để học tốt về hình chóp tứ giác đều, bạn cần:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Hình chóp tứ giác đều SGK Toán 8 Cánh diều. Chúc bạn học tập tốt!