Chào mừng bạn đến với bài học về Lý thuyết Hình đồng dạng trong chương trình Toán 8 Cánh Diều tại giaitoan.edu.vn. Đây là một trong những chủ đề quan trọng, đặt nền móng cho các kiến thức hình học nâng cao hơn.
Chúng tôi cung cấp lý thuyết đầy đủ, dễ hiểu, kèm theo các ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức một cách hiệu quả nhất.
Hình đồng dạng là gì?
1. Hình đồng dạng phối cảnh (hình vị tự)
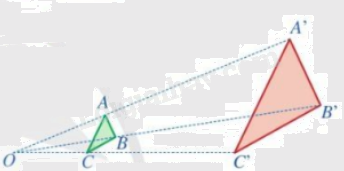
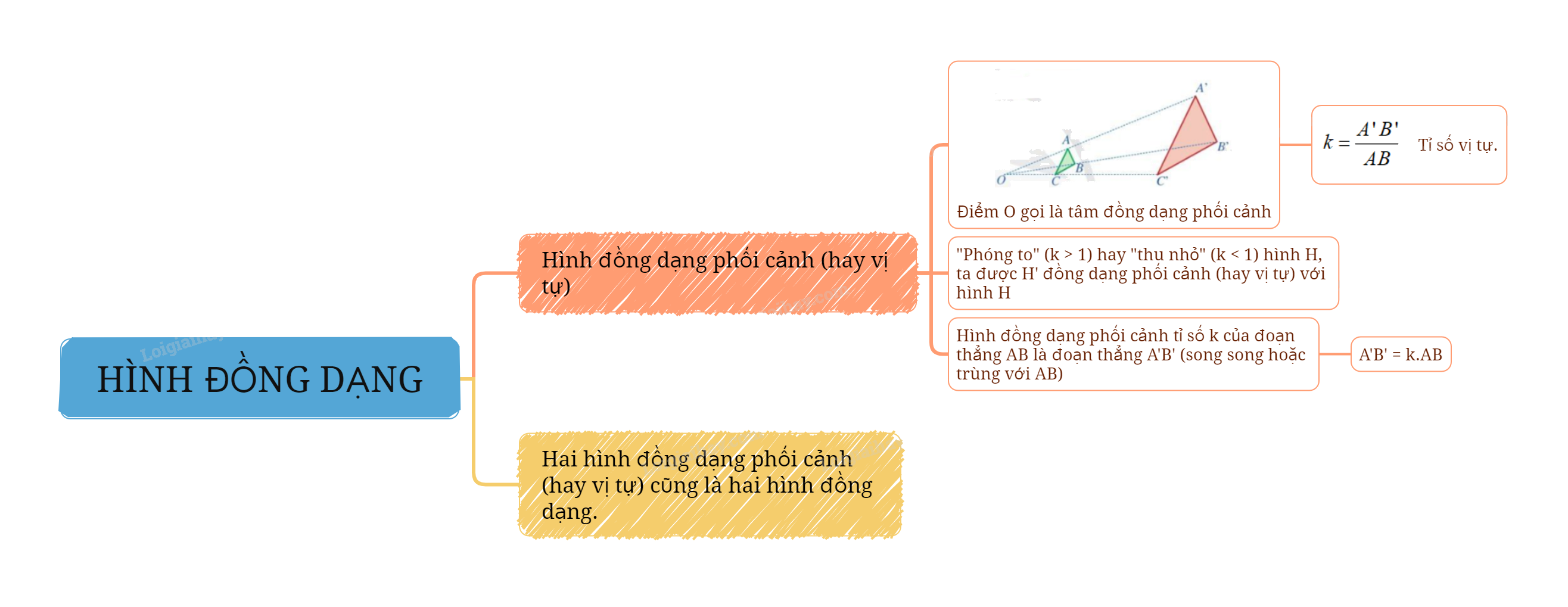
Hai tam giác A’B’C’ và ABC gọi là đồng dạng phối cảnh (hay vị tự) với nhau, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số \(k = \frac{{A'B'}}{{AB}}\) gọi là tỉ số vị tự.
Tổng quát:
Bằng cách “phóng to” (nếu tỉ số vị tự k > 1) hay “thu nhỏ” (nếu tỉ số vị tự k < 1) hình H, ta sẽ nhận được hình H’đồng dạng phối cảnh (hay vị tự) với hình H.
Ta gọi hình H’ là hình đồng dạng phối cảnh (hay vị tự) tỉ số k của hình H.
Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng AB là một đoạn thẳng A’B’ (nằm trên đường thẳng song song hoặc trùng với đường thẳng AB) và \(A'B'{\rm{ }} = {\rm{ }}k.AB\)
2. Hình đồng dạng
Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
Hình đồng dạng là một khái niệm quan trọng trong hình học, giúp chúng ta hiểu về mối quan hệ giữa các hình có kích thước khác nhau nhưng có hình dạng tương tự. Trong chương trình Toán 8 Cánh Diều, việc nắm vững lý thuyết hình đồng dạng là chìa khóa để giải quyết nhiều bài toán thực tế và nâng cao khả năng tư duy logic.
Hai hình được gọi là đồng dạng với nhau nếu chúng có cùng hình dạng nhưng khác kích thước. Điều này có nghĩa là, nếu ta phóng to hoặc thu nhỏ một hình, ta sẽ được một hình đồng dạng với hình ban đầu.
Tỉ số đồng dạng của hai hình đồng dạng là tỉ số giữa hai đoạn thẳng tương ứng trên hai hình đó. Tỉ số đồng dạng thường được ký hiệu là k. Nếu hai hình A và B đồng dạng với nhau, ta có thể viết A ~ B và tỉ số đồng dạng là k, nghĩa là:
Có ba trường hợp đồng dạng của tam giác:
Khi hai tam giác đồng dạng, các cạnh tương ứng tỉ lệ và các góc tương ứng bằng nhau. Điều này có nghĩa là:
Lý thuyết hình đồng dạng có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức về hình đồng dạng, hãy thực hành giải các bài tập sau:
| Bài tập | Mô tả |
|---|---|
| Bài 1 | Cho tam giác ABC và tam giác A'B'C' có AB = 3cm, BC = 4cm, CA = 5cm và A'B' = 6cm, B'C' = 8cm, C'A' = 10cm. Chứng minh rằng ΔABC ~ ΔA'B'C'. |
| Bài 2 | Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm. Gọi D là điểm sao cho ΔABC ~ ΔDBA. Tính độ dài AD. |
Lý thuyết hình đồng dạng là một phần quan trọng của chương trình Toán 8 Cánh Diều. Việc hiểu rõ các định nghĩa, tính chất và ứng dụng của hình đồng dạng sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả và phát triển tư duy logic.
Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để nắm vững chủ đề này nhé!