Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 71, 72 sách giáo khoa Toán 8 tập 1 chương trình Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và trình bày một cách rõ ràng nhất để hỗ trợ tối đa cho quá trình học tập của các em.
Xét hàm số: y = x – 2 a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau: x 0 2 3 y ? ? ? b) Vẽ các điểm A (0; -2); B(2; 0); C(3; 1) của đồ thị hàm số y = x – 2 trong mặt phẳng tọa độ Oxy. Dùng thước thẳng để kiểm tra ba điểm A, B, C có thẳng hàng hay không?
Video hướng dẫn giải
Cho hàm số y = 4x + 3. Tìm điểm thuộc đồ thị hàm số của hàm số có hoành độ bằng 0.
Phương pháp giải:
Thay giá trị x = 0 vào công thức hàm số y = 4x + 3
Lời giải chi tiết:
Với x = 0 thì y = 4.0 + 3 = 3
Vậy điểm có hoành độ bằng 0 thuộc đồ thị hàm số y = 4x + 3 là (0; 3)
Video hướng dẫn giải
Xét hàm số: y = x – 2
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
x | 0 | 2 | 3 |
y | ? | ? | ? |
b) Vẽ các điểm A (0; -2); B(2; 0); C(3; 1) của đồ thị hàm số y = x – 2 trong mặt phẳng tọa độ Oxy. Dùng thước thẳng để kiểm tra ba điểm A, B, C có thẳng hàng hay không?
Phương pháp giải:
Thay các giá trị x = 0; x = 2; x = 3 vào công thức đồ thị hàm số y = x – 2
Lời giải chi tiết:
a) Thay các giá trị x = 0; x = 2; x = 3 vào công thức đồ thị hàm số y = x – 2 ta được các giá trị y tương ứng ở bảng sau:
x | 0 | 2 | 3 |
y | -2 | 0 | 1 |
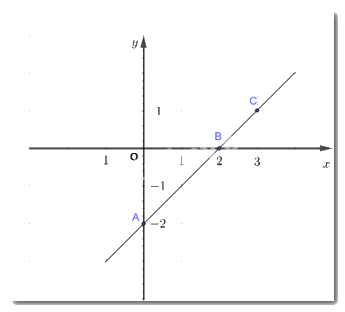
b) Vẽ các điểm A (0; -2); B(2; 0); C(3; 0)
Kẻ đường thẳng qua điểm A và C ta thấy đường thẳng đi qua điểm B
Ba điểm A, B, C có thẳng hàng
Video hướng dẫn giải
Xét hàm số: y = x – 2
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
x | 0 | 2 | 3 |
y | ? | ? | ? |
b) Vẽ các điểm A (0; -2); B(2; 0); C(3; 1) của đồ thị hàm số y = x – 2 trong mặt phẳng tọa độ Oxy. Dùng thước thẳng để kiểm tra ba điểm A, B, C có thẳng hàng hay không?
Phương pháp giải:
Thay các giá trị x = 0; x = 2; x = 3 vào công thức đồ thị hàm số y = x – 2
Lời giải chi tiết:
a) Thay các giá trị x = 0; x = 2; x = 3 vào công thức đồ thị hàm số y = x – 2 ta được các giá trị y tương ứng ở bảng sau:
x | 0 | 2 | 3 |
y | -2 | 0 | 1 |
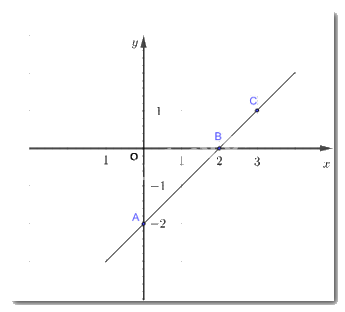
b) Vẽ các điểm A (0; -2); B(2; 0); C(3; 0)
Kẻ đường thẳng qua điểm A và C ta thấy đường thẳng đi qua điểm B
Ba điểm A, B, C có thẳng hàng
Video hướng dẫn giải
Cho hàm số y = 4x + 3. Tìm điểm thuộc đồ thị hàm số của hàm số có hoành độ bằng 0.
Phương pháp giải:
Thay giá trị x = 0 vào công thức hàm số y = 4x + 3
Lời giải chi tiết:
Với x = 0 thì y = 4.0 + 3 = 3
Vậy điểm có hoành độ bằng 0 thuộc đồ thị hàm số y = 4x + 3 là (0; 3)
Mục 1 trang 71, 72 SGK Toán 8 tập 1 - Cánh diều thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Đây là một phần quan trọng trong việc xây dựng nền tảng kiến thức đại số cho học sinh. Việc nắm vững các kiến thức và kỹ năng trong mục này sẽ giúp học sinh giải quyết các bài toán phức tạp hơn trong tương lai.
Mục 1 tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán với đa thức, bao gồm:
Bài 1 yêu cầu học sinh thực hiện các phép toán cộng, trừ đa thức. Để giải bài này, học sinh cần chú ý đến việc nhóm các hạng tử đồng dạng và thực hiện các phép toán một cách cẩn thận.
Ví dụ:
(3x2 + 2x - 1) + (x2 - 3x + 2) = (3x2 + x2) + (2x - 3x) + (-1 + 2) = 4x2 - x + 1
Bài 2 yêu cầu học sinh thực hiện các phép toán nhân đa thức. Để giải bài này, học sinh cần áp dụng quy tắc nhân đa thức với đa thức, tức là nhân mỗi hạng tử của đa thức này với mỗi hạng tử của đa thức kia, sau đó cộng các kết quả lại.
Ví dụ:
(x + 2)(x - 3) = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6
Bài 3 yêu cầu học sinh sử dụng các hằng đẳng thức đáng nhớ để biến đổi và rút gọn biểu thức đại số. Học sinh cần nắm vững các hằng đẳng thức như (a + b)2 = a2 + 2ab + b2, (a - b)2 = a2 - 2ab + b2, a2 - b2 = (a + b)(a - b) để giải bài này.
Ví dụ:
x2 + 4x + 4 = (x + 2)2
Để học tốt môn Toán 8, đặc biệt là phần đại số, học sinh cần:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Mục 1 trang 71, 72 SGK Toán 8 tập 1 - Cánh diều. Chúc các em học tập tốt!