Chào mừng bạn đến với bài học lý thuyết về phép cộng, phép trừ phân thức đại số trong chương trình Toán 8, sách Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng, các quy tắc quan trọng và ví dụ minh họa để bạn có thể hiểu rõ và vận dụng thành thạo kiến thức này.
Chúng tôi tại giaitoan.edu.vn luôn cố gắng mang đến những bài giảng chất lượng, dễ hiểu và phù hợp với từng đối tượng học sinh. Hãy cùng bắt đầu khám phá thế giới của phân thức đại số!
Cộng, trừ hai phân thức cùng mẫu như thế nào?
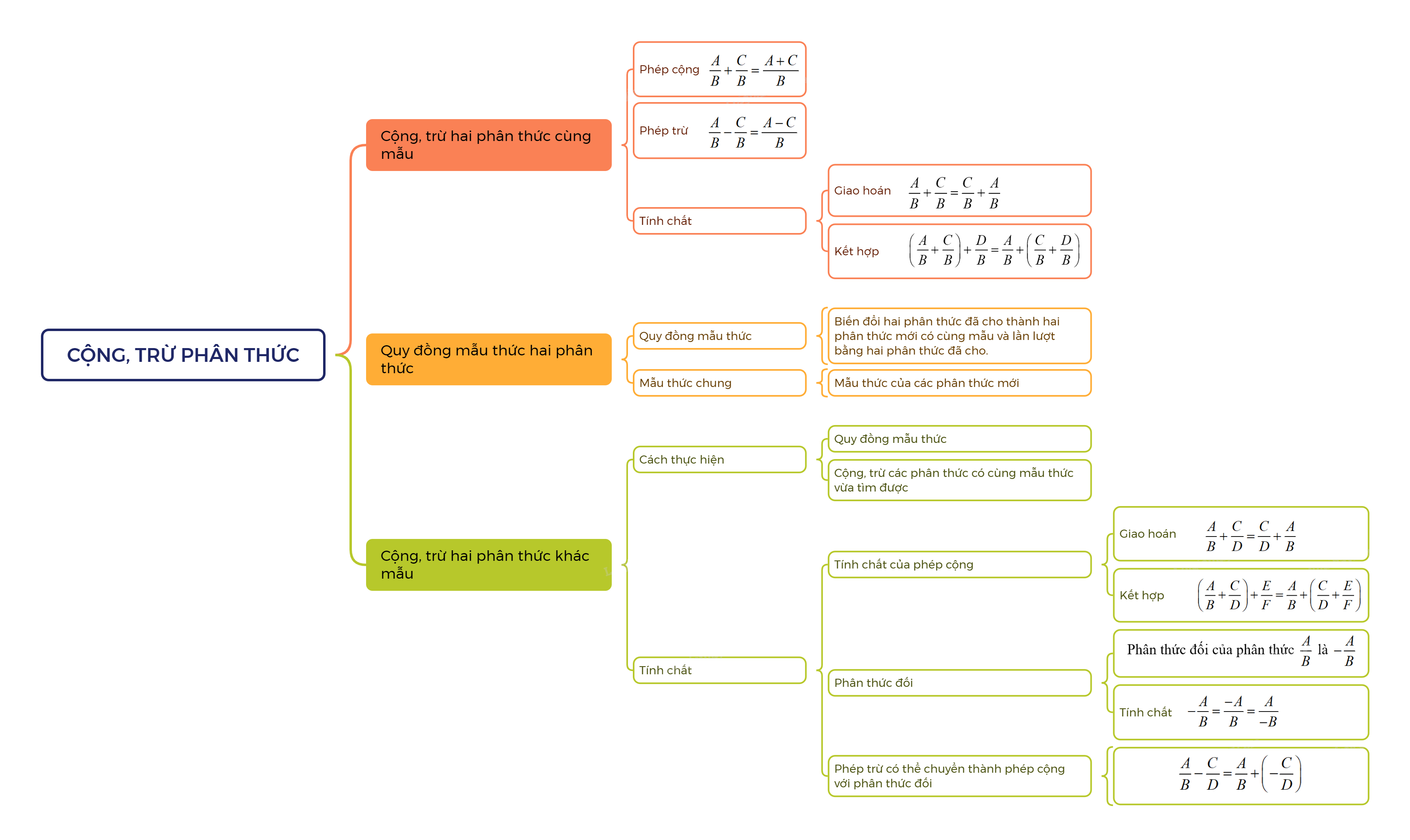
1. Cộng, trừ hai phân thức cùng mẫu
Muốn cộng (hoặc trừ) hai phân thức có cùng mẫu thức, ta cộng (hoặc trừ) các tử thức với nhau và giữ nguyên mẫu thức.
\(\frac{A}{B} + \frac{C}{B} = \frac{{A + C}}{B}; \frac{A}{B} - \frac{C}{B} = \frac{{A - C}}{B}\)
Chú ý: Phép cộng phân thức có các tính chất giao hoán, kết hợp tương tự như đối với phân số.
Ví dụ:
\(\begin{array}{l}\frac{{x + y}}{{xy}} + \frac{{x - y}}{{xy}} = \frac{{x + y + x - y}}{{xy}} = \frac{{2x}}{{xy}} = \frac{2}{y}\\\frac{x}{{x + 3}} + \frac{{2 - x}}{{x + 3}} = \frac{{x + 2 - x}}{{x + 3}} = \frac{2}{{x + 3}}\end{array}\)
2. Cộng, trừ hai phân thức khác mẫu
Quy đồng mẫu thức hai phân thức
Quy đồng mẫu thức hai phân thức là biến đổi hai phân thức đã cho thành hai phân thức mới có cùng mẫu thức và lần lượt bằng hai mẫu thức đã cho.
Mẫu thức chung
Mẫu thức của các phân thức mới đó gọi là mẫu thức chung của hai phân thức đã cho.
Cộng, trừ hai phân thức khác mẫu
Muốn cộng, trừ hai phân thức khác mẫu thức, ta thực hiện các bước:
- Quy đồng mẫu thức;
- Cộng, trừ các phân thức có cùng mẫu thức vừa tìm được.
Chú ý:
a. Phép cộng các phân thức cũng có các tính chất giao hoán, kết hợp:
\(\frac{A}{B} + \frac{C}{D} = \frac{C}{D} + \frac{A}{B}; \left( {\frac{A}{B} + \frac{C}{D}} \right) + \frac{E}{F} = \frac{A}{B} + \left( {\frac{C}{D} + \frac{E}{F}} \right)\).
b. Phân thức đối của phân thức \(\frac{A}{B}\) là \( - \frac{A}{B}\). Ta có tính chất \( - \frac{A}{B} = \frac{{ - A}}{B} = \frac{A}{{ - B}}\,\).
c. Phép trừ phân thức có thể chuyển thành phép cộng với phân thức đối: \(\frac{A}{B} - \frac{C}{D} = \frac{A}{B} + \left( { - \frac{C}{D}} \right)\)
Phân thức đại số là một khái niệm quan trọng trong chương trình Toán học lớp 8. Việc nắm vững lý thuyết về phép cộng, phép trừ phân thức đại số là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và các bài tập vận dụng để giúp bạn hiểu rõ hơn về chủ đề này.
Một phân thức đại số là một biểu thức có dạng P/Q, trong đó P và Q là các đa thức, và Q khác 0. P được gọi là tử số, Q được gọi là mẫu số.
Một phân thức đại số chỉ xác định khi mẫu số khác 0. Điều này có nghĩa là chúng ta cần tìm các giá trị của biến sao cho mẫu số không bằng 0.
Để cộng hai phân thức đại số, chúng ta cần thực hiện các bước sau:
Công thức tổng quát:
P/Q + R/S = (PS + QR) / QS (với Q và S khác 0)
Tương tự như phép cộng, để trừ hai phân thức đại số, chúng ta thực hiện các bước sau:
Công thức tổng quát:
P/Q - R/S = (PS - QR) / QS (với Q và S khác 0)
Ví dụ 1: Tính 1/x + 2/y
MSC: xy
1/x + 2/y = y/xy + 2x/xy = (y + 2x) / xy
Ví dụ 2: Tính 3/(x+1) - 2/(x-1)
MSC: (x+1)(x-1)
3/(x+1) - 2/(x-1) = 3(x-1)/((x+1)(x-1)) - 2(x+1)/((x+1)(x-1)) = (3x - 3 - 2x - 2) / ((x+1)(x-1)) = (x - 5) / ((x+1)(x-1))
Hãy thực hành giải các bài tập sau để củng cố kiến thức:
Khi thực hiện phép cộng, phép trừ phân thức đại số, cần chú ý:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết phép cộng, phép trừ phân thức đại số. Chúc bạn học tập tốt!