Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 71 sách giáo khoa Toán 8 Cánh diều. Bài viết này cung cấp đáp án chính xác, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và đầy đủ lời giải các bài tập Toán 8, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
Cho
Video hướng dẫn giải
Cho\(\Delta A'B'C' \backsim \Delta ABC\)và \(AB = 3,\,\,BC = 2,\,\,CA = 4,\,\,A'B' = x,\,\,B'C' = 3,\,\,C'A' = y\). Tìm \(x\) và \(y\).
Phương pháp giải:
Sử dụng định nghĩa tam giác đồng dạng để tìm \(x\) và \(y\).
Lời giải chi tiết:
Vì \(\Delta A'B'C' \backsim \Delta ABC\)nên ta có:
\(\left\{ \begin{array}{l}A'B' = AB = 3\\B'C' = BC = 2\end{array} \right.\)
Vậy \(x = 3\) và \(y = 2\).
Video hướng dẫn giải
Cho tam giác ABC, điểm M nằm trên cạnh BC. Gọi A', B', C' lần lượt là trung điểm của các đoạn thẳng MA, MB, MC (Hình 47)
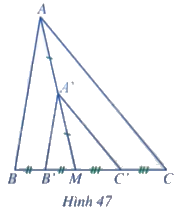
a) So sánh các cặp góc:
\( \widehat {B'A'C'} \) và \( \widehat {BAC} \); \( \widehat {C'B'A'} \) và \( \widehat {CBA} \); \( \widehat {A'C'B'} \) và \( \widehat {ACB} \).
b) So sánh các tỉ số: \( \frac{A'B'}{AB} \); \( \frac{B'C'}{BC} \); \( \frac{C'A'}{CA} \).
Phương pháp giải:
a) Dựa vào tính chất đường trung bình của tam giác để so sánh các góc.
Sử dụng tính chất tổng các góc trong tam giác bằng \(180^0\)
b) Dựa vào tính chất đường trung bình để so sánh.
Lời giải chi tiết:
a) Xét tam giác ABM có A'B' là đường trung bình của tam giác
\( \Rightarrow A'B' // AB\)
\( \Rightarrow \widehat {C'B'A'} = \widehat {CBA}\) (hai góc đồng vị)
Tương tự, tam giác AMC có A'C' là đường trung bình nên \( \widehat {A'C'B'} = \widehat {ACB}\) (hai góc đồng vị)
Xét tam giác ABC có:
\( \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = 180^0\)
Xét tam giác A'B'C' có:
\( \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'} = 180^0\)
\(\Rightarrow \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'}\)
\(\Rightarrow \widehat {BAC} = \widehat {B'A'C'}\)
b) A'B' là đường trung bình của tam giác ABM nên
\(A'B' = \frac {1}{2} AB \Rightarrow \frac {A'B'}{AB} = \frac {1}{2}\)
A'B' là đường trung bình của tam giác ABM nên
\(A'C' = \frac {1}{2} AC \Rightarrow \frac {A'C'}{AC} = \frac {1}{2}\)
Ta có: \( \frac{B'C'}{BC} = \frac{MB' +MC'}{2MB' + 2MC'} = \frac{MB' +MC'}{2(MB' + MC')} = \frac{1}{2}\)
\( \Rightarrow \frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{C'A'}{CA} \)
Video hướng dẫn giải
Cho\(\Delta A'B'C' \backsim \Delta ABC\)và \(AB = 3,\,\,BC = 2,\,\,CA = 4,\,\,A'B' = x,\,\,B'C' = 3,\,\,C'A' = y\). Tìm \(x\) và \(y\).
Phương pháp giải:
Sử dụng định nghĩa tam giác đồng dạng để tìm \(x\) và \(y\).
Lời giải chi tiết:
Vì \(\Delta A'B'C' \backsim \Delta ABC\)nên ta có:
\(\left\{ \begin{array}{l}A'B' = AB = 3\\B'C' = BC = 2\end{array} \right.\)
Vậy \(x = 3\) và \(y = 2\).
Video hướng dẫn giải
Cho tam giác ABC, điểm M nằm trên cạnh BC. Gọi A', B', C' lần lượt là trung điểm của các đoạn thẳng MA, MB, MC (Hình 47)
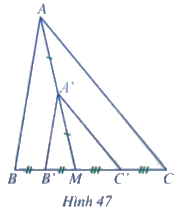
a) So sánh các cặp góc:
\( \widehat {B'A'C'} \) và \( \widehat {BAC} \); \( \widehat {C'B'A'} \) và \( \widehat {CBA} \); \( \widehat {A'C'B'} \) và \( \widehat {ACB} \).
b) So sánh các tỉ số: \( \frac{A'B'}{AB} \); \( \frac{B'C'}{BC} \); \( \frac{C'A'}{CA} \).
Phương pháp giải:
a) Dựa vào tính chất đường trung bình của tam giác để so sánh các góc.
Sử dụng tính chất tổng các góc trong tam giác bằng \(180^0\)
b) Dựa vào tính chất đường trung bình để so sánh.
Lời giải chi tiết:
a) Xét tam giác ABM có A'B' là đường trung bình của tam giác
\( \Rightarrow A'B' // AB\)
\( \Rightarrow \widehat {C'B'A'} = \widehat {CBA}\) (hai góc đồng vị)
Tương tự, tam giác AMC có A'C' là đường trung bình nên \( \widehat {A'C'B'} = \widehat {ACB}\) (hai góc đồng vị)
Xét tam giác ABC có:
\( \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = 180^0\)
Xét tam giác A'B'C' có:
\( \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'} = 180^0\)
\(\Rightarrow \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'}\)
\(\Rightarrow \widehat {BAC} = \widehat {B'A'C'}\)
b) A'B' là đường trung bình của tam giác ABM nên
\(A'B' = \frac {1}{2} AB \Rightarrow \frac {A'B'}{AB} = \frac {1}{2}\)
A'B' là đường trung bình của tam giác ABM nên
\(A'C' = \frac {1}{2} AC \Rightarrow \frac {A'C'}{AC} = \frac {1}{2}\)
Ta có: \( \frac{B'C'}{BC} = \frac{MB' +MC'}{2MB' + 2MC'} = \frac{MB' +MC'}{2(MB' + MC')} = \frac{1}{2}\)
\( \Rightarrow \frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{C'A'}{CA} \)
Mục 1 trang 71 SGK Toán 8 – Cánh diều thường xoay quanh các bài tập về ứng dụng của phương pháp cộng, trừ, nhân, chia đa thức. Để giải quyết hiệu quả các bài toán này, học sinh cần nắm vững các kiến thức cơ bản về đa thức, các phép toán trên đa thức và các quy tắc biến đổi đại số.
Thông thường, mục 1 trang 71 sẽ bao gồm các dạng bài tập sau:
Để giải quyết các bài tập trong mục 1 trang 71 SGK Toán 8 – Cánh diều một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Rút gọn biểu thức sau: (3x + 2)(x - 1) - (x + 3)(2x - 1)
Giải:
(3x + 2)(x - 1) - (x + 3)(2x - 1) = (3x2 - 3x + 2x - 2) - (2x2 - x + 6x - 3)
= 3x2 - x - 2 - 2x2 - 5x + 3
= (3x2 - 2x2) + (-x - 5x) + (-2 + 3)
= x2 - 6x + 1
Để củng cố kiến thức và kỹ năng giải bài tập về đa thức, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập, đề thi thử hoặc các trang web học toán online.
Giaitoan.edu.vn cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để học Toán 8 hiệu quả và đạt kết quả cao!