Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 39, 40 sách giáo khoa Toán 8 – Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong bài toán nêu ở phần mở đầu, hãy viết:
Video hướng dẫn giải
Khi \(x = 4\), tính giá trị mỗi vế của phương trình: \(3x + 4 = x + 12\,\,\left( 1 \right)\). So sánh hai giá trị đó.
Phương pháp giải:
Thay \(x = 4\) vào từng vế của phương trình rồi tính giá trị mỗi vế.
Lời giải chi tiết:
Thay \(x = 4\) vào vế trái của phương trình ta được: \(3.4 + 4 = 12 + 4 = 16\).
Thay \(x = 4\) vào vế phải của phương trình ta được: \(4 + 12 = 16\).
Ta thấy khi \(x = 4\), hai vế của phương trình có giá trị bằng nhau.
Video hướng dẫn giải
Trong bài toán nêu ở phần mở đầu, hãy viết:
a) Các biểu thức \(A\left( x \right),\,\,B\left( x \right)\) lần lượt biểu thị (theo \(x\)) tổng khối lượng các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải;
b) Hệ thức thể hiện sự bằng nhau của hai biểu thức trên.
Phương pháp giải:
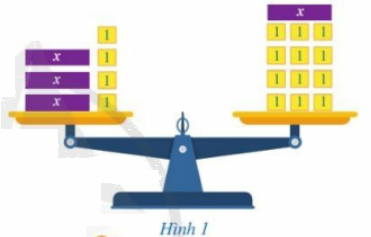
Dựa theo số lượng các hộp màu tím và hộp màu vàng ở hai bên cân để viết biểu thức \(A\left( x \right),\,\,B\left( x \right)\) biểu thị (theo \(x\)) tổng khối lượng ở mỗi đĩa cân.
Lời giải chi tiết:
a)
- Ta thấy ở đĩa cân bên trái có 3 hộp màu tím mỗi hộp có khối lượng \(x\) kg và 4 hộp màu vàng mỗi hộp có khối lượng 1 kg nên biểu thức biểu diễn tổng khối lượng các hộp xếp ở đĩa cân bên trái là:
\(\begin{array}{l}\,\,\,\,\,\,\,A\left( x \right) = 3.x + 4.1\\ \Rightarrow A\left( x \right) = 3x + 4\end{array}\)
- Ta thấy ở đĩa cân bên phải có 1 hộp màu tím mỗi hộp có khối lượng \(x\) kg và 12 hộp màu vàng mỗi hộp có khối lượng 1 kg nên biểu thức biểu diễn tổng khối lượng các hộp xếp ở đĩa cân bên phải là:
\(\begin{array}{l}\,\,\,\,\,\,B\left( x \right) = 1.x + 12.1\\ \Rightarrow B\left( x \right) = x + 12\end{array}\)
b) Biểu thức thể hiện sự bằng nhau của hai biểu thức trên là: \(3x + 4 = x + 12\)
Video hướng dẫn giải
Trong bài toán nêu ở phần mở đầu, hãy viết:
a) Các biểu thức \(A\left( x \right),\,\,B\left( x \right)\) lần lượt biểu thị (theo \(x\)) tổng khối lượng các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải;
b) Hệ thức thể hiện sự bằng nhau của hai biểu thức trên.
Phương pháp giải:
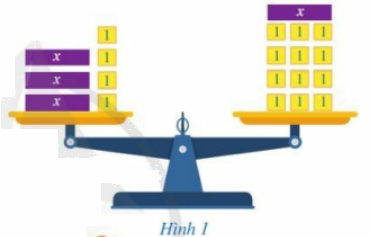
Dựa theo số lượng các hộp màu tím và hộp màu vàng ở hai bên cân để viết biểu thức \(A\left( x \right),\,\,B\left( x \right)\) biểu thị (theo \(x\)) tổng khối lượng ở mỗi đĩa cân.
Lời giải chi tiết:
a)
- Ta thấy ở đĩa cân bên trái có 3 hộp màu tím mỗi hộp có khối lượng \(x\) kg và 4 hộp màu vàng mỗi hộp có khối lượng 1 kg nên biểu thức biểu diễn tổng khối lượng các hộp xếp ở đĩa cân bên trái là:
\(\begin{array}{l}\,\,\,\,\,\,\,A\left( x \right) = 3.x + 4.1\\ \Rightarrow A\left( x \right) = 3x + 4\end{array}\)
- Ta thấy ở đĩa cân bên phải có 1 hộp màu tím mỗi hộp có khối lượng \(x\) kg và 12 hộp màu vàng mỗi hộp có khối lượng 1 kg nên biểu thức biểu diễn tổng khối lượng các hộp xếp ở đĩa cân bên phải là:
\(\begin{array}{l}\,\,\,\,\,\,B\left( x \right) = 1.x + 12.1\\ \Rightarrow B\left( x \right) = x + 12\end{array}\)
b) Biểu thức thể hiện sự bằng nhau của hai biểu thức trên là: \(3x + 4 = x + 12\)
Video hướng dẫn giải
Khi \(x = 4\), tính giá trị mỗi vế của phương trình: \(3x + 4 = x + 12\,\,\left( 1 \right)\). So sánh hai giá trị đó.
Phương pháp giải:
Thay \(x = 4\) vào từng vế của phương trình rồi tính giá trị mỗi vế.
Lời giải chi tiết:
Thay \(x = 4\) vào vế trái của phương trình ta được: \(3.4 + 4 = 12 + 4 = 16\).
Thay \(x = 4\) vào vế phải của phương trình ta được: \(4 + 12 = 16\).
Ta thấy khi \(x = 4\), hai vế của phương trình có giá trị bằng nhau.
Mục 1 trang 39, 40 SGK Toán 8 – Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, nghiệm của đa thức và các phép toán trên đa thức. Đây là một phần quan trọng trong chương trình học Toán 8, giúp học sinh chuẩn bị cho các kiến thức nâng cao hơn ở các chương sau.
Bài tập này yêu cầu học sinh thu gọn các đa thức đã cho bằng cách thực hiện các phép cộng, trừ các đơn thức đồng dạng. Để thu gọn đa thức, ta cần:
Ví dụ: Thu gọn đa thức 3x2 + 2x - 5x2 + x + 1. Ta có:
3x2 - 5x2 + 2x + x + 1 = (3 - 5)x2 + (2 + 1)x + 1 = -2x2 + 3x + 1
Bài tập này yêu cầu học sinh tìm bậc của các đa thức đã cho. Bậc của đa thức là số mũ lớn nhất của biến trong đa thức đó.
Ví dụ: Tìm bậc của đa thức -2x2 + 3x + 1. Bậc của đa thức này là 2.
Bài tập này yêu cầu học sinh xác định hệ số của một biến cụ thể trong đa thức. Hệ số của một biến là số nhân với biến đó.
Ví dụ: Xác định hệ số của x2 trong đa thức -2x2 + 3x + 1. Hệ số của x2 là -2.
Bài tập này yêu cầu học sinh tính giá trị của đa thức khi biết giá trị của biến. Để tính giá trị của đa thức, ta thay giá trị của biến vào đa thức và thực hiện các phép tính.
Ví dụ: Tính giá trị của đa thức -2x2 + 3x + 1 khi x = 2. Ta có:
-2(2)2 + 3(2) + 1 = -2(4) + 6 + 1 = -8 + 6 + 1 = -1
Khi giải bài tập về đa thức, cần chú ý đến các quy tắc về dấu và các phép toán trên số. Ngoài ra, cần rèn luyện kỹ năng biến đổi đa thức để giải quyết các bài tập phức tạp hơn.
Để củng cố kiến thức và rèn luyện kỹ năng, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc học Toán 8 và đạt kết quả tốt nhất. Chúc các em học tập tốt!