Bài học này cung cấp lý thuyết đầy đủ và chi tiết về tính chất đường phân giác của tam giác, thuộc chương trình Toán 8 sách Cánh Diều.
Chúng ta sẽ cùng tìm hiểu định nghĩa, các tính chất quan trọng và cách áp dụng chúng vào giải các bài tập thực tế.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán!
Đường phân giác của tam giác có tính chất gì?
Định lí
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
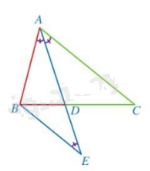
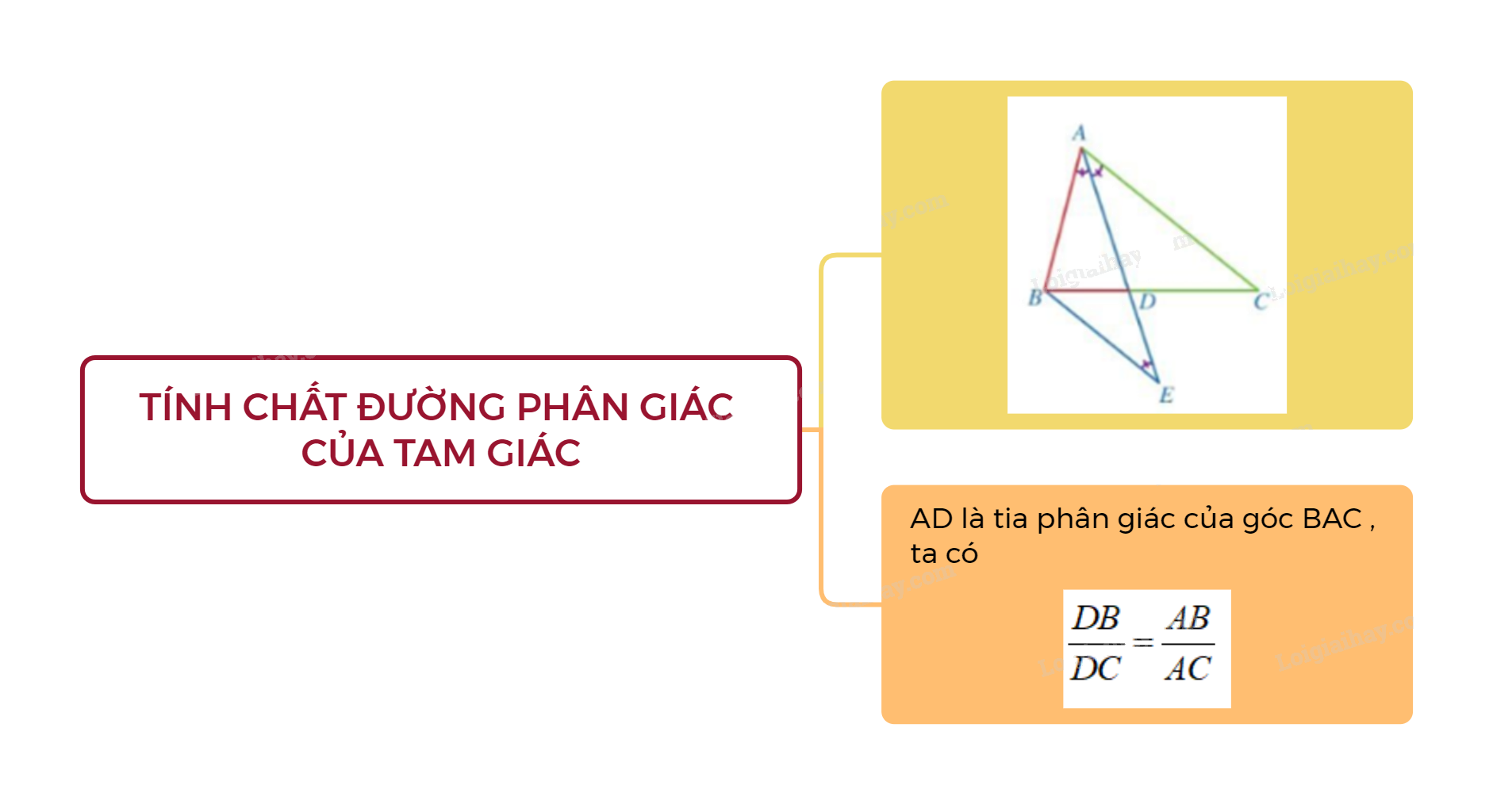
AD là đường phân giác của góc A trong \(\Delta ABC\), \(D \in BC\)
\( \Rightarrow \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\)
Ví dụ:
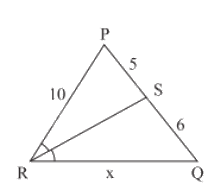
RS là tia phân giác của góc \(\widehat {PRQ}\). Sử dụng tính chất đường phân giác, ta có:
\(\begin{array}{l}\frac{{SQ}}{{SR}} = \frac{{RQ}}{{RP}}\\ \Leftrightarrow \frac{{10}}{5} = \frac{x}{6}\\ \Leftrightarrow 2 = \frac{x}{6}\\ \Leftrightarrow x = 12\end{array}\)
Vậy độ dài đoạn thẳng RQ là 12.
Đường phân giác của một tam giác là đoạn thẳng nối đỉnh của tam giác với điểm chia cạnh đối diện thành hai đoạn thẳng bằng nhau. Trong tam giác ABC, nếu AD là đường phân giác (D thuộc BC) thì BD = CD.
Tính chất quan trọng nhất của đường phân giác là:
Cụ thể, trong tam giác ABC, với AD là đường phân giác (D thuộc BC), ta có:
AB/AC = BD/DC
Chứng minh: (Có thể trình bày chứng minh bằng cách sử dụng định lý Thales hoặc các phương pháp chứng minh tam giác đồng dạng)
Từ tính chất trên, ta có thể suy ra một số hệ quả hữu ích:
Cho tam giác ABC có AB = 5cm, AC = 7cm, và AD là đường phân giác (D thuộc BC). Tính tỉ số BD/DC.
Giải:
Áp dụng tính chất đường phân giác, ta có:
BD/DC = AB/AC = 5/7
1. Cho tam giác ABC có AB = 6cm, BC = 8cm, CA = 10cm. Gọi AD là đường phân giác của góc BAC (D thuộc BC). Tính độ dài BD và DC.
2. Cho tam giác MNP có MN = 4cm, NP = 6cm, MP = 5cm. Gọi NI là đường phân giác của góc MNP (I thuộc MP). Tính tỉ số MI/IP.
3. Trong tam giác ABC, đường phân giác AD chia cạnh BC thành hai đoạn BD và DC tỉ lệ với 2 và 3. Biết AB = 4cm. Tính độ dài AC.
Khi giải các bài toán liên quan đến đường phân giác, cần chú ý:
Ngoài tính chất đường phân giác, còn có một số khái niệm và tính chất liên quan khác như:
Việc nắm vững các khái niệm và tính chất này sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả hơn.
Lý thuyết về tính chất đường phân giác của tam giác là một kiến thức cơ bản và quan trọng trong chương trình Toán 8. Việc hiểu rõ và vận dụng thành thạo lý thuyết này sẽ giúp bạn tự tin giải quyết các bài toán liên quan và đạt kết quả tốt trong môn học.