Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 60 SGK Toán 8 Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 8.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, giảm bớt gánh nặng trong quá trình học tập.
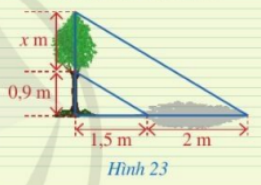
Người ta đo bóng của một cây và được các số đo ở Hình 23.
Đề bài
Người ta đo bóng của một cây và được các số đo ở Hình 23. Giả sử rằng các tia nắng song song với nhau, hãy tính độ cao \(x\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định lý Thales để tính độ cao \(x\).
Lời giải chi tiết
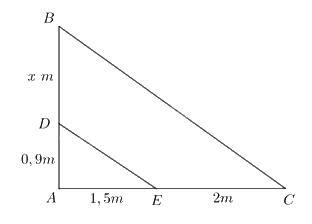
Đoạn thẳng AB biểu thị cho độ cao của cây, đoạn thẳng AD và DB biểu thị độ cao của thân và tán cây, đoạn thẳng AE và EC biểu thị độ dài cái bóng của thân cây và tán cây, đoạn thẳng DE và BC biểu thị cho các tia nắng.
Xét tam giác ABC với \(DE\parallel BC\) ta có:
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) (Định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{0,9}}{x} = \frac{{1,5}}{2}\\ \Rightarrow 0,9.2 = 1,5x\\ \Rightarrow 1,8 = 1,5x\\ \Rightarrow x = 1,2\end{array}\)
Vậy độ cao \(x\) là 1,2 m.
Mục 2 trang 60 SGK Toán 8 – Cánh diều tập trung vào việc vận dụng các kiến thức đã học về hình hộp chữ nhật và hình lập phương để giải các bài toán thực tế. Các bài tập trong mục này thường yêu cầu học sinh tính thể tích, diện tích bề mặt của các hình, hoặc xác định mối quan hệ giữa các yếu tố của hình.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 60, chúng tôi sẽ trình bày chi tiết lời giải của từng bài tập:
Lời giải:
Thể tích của hình hộp chữ nhật được tính theo công thức V = a.b.c, trong đó a là chiều dài, b là chiều rộng và c là chiều cao.
Thay số vào công thức, ta có: V = 5cm . 4cm . 3cm = 60cm3
Vậy thể tích của hình hộp chữ nhật là 60cm3.
Lời giải:
Diện tích bề mặt của hình lập phương được tính theo công thức S = 6a2, trong đó a là cạnh của hình lập phương.
Thay số vào công thức, ta có: S = 6 . (2cm)2 = 6 . 4cm2 = 24cm2
Vậy diện tích bề mặt của hình lập phương là 24cm2.
Lời giải:
Thể tích của bể nước hình hộp chữ nhật được tính theo công thức V = a.b.c, trong đó a là chiều dài, b là chiều rộng và c là chiều cao.
Thay số vào công thức, ta có: V = 1.2m . 0.8m . 1m = 0.96m3
Vậy thể tích của bể nước là 0.96m3.
Kiến thức về hình hộp chữ nhật và hình lập phương có ứng dụng rộng rãi trong thực tế, như:
Hy vọng với bài giải chi tiết và hướng dẫn giải bài tập mục 2 trang 60 SGK Toán 8 – Cánh diều, các em đã nắm vững kiến thức và kỹ năng giải các bài toán về hình hộp chữ nhật và hình lập phương. Chúc các em học tập tốt!