Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 118 SGK Toán 8 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập này thuộc chương trình học Toán 8 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng các kiến thức đã học vào thực tế.
a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không? b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 69)
Video hướng dẫn giải
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy điểm D, E sao cho: BD = DE = EC
Qua D và E kẻ đường thẳng vuông góc với BC, chúng cắt AB và AC lần lượt tại H và G. Chứng minh tứ giác DEGH là hình vuông.
Phương pháp giải:
Chứng minh tứ giác DEGH là hình chữ nhật có HD = DE
Lời giải chi tiết:
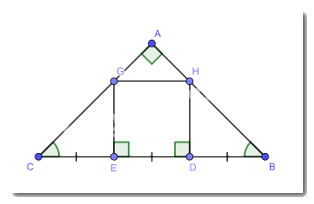
Xét \(\Delta ABC\) vuông cân tại A
\( \Rightarrow \widehat {ABC} = \widehat {ACB} = {45^0}\)
Xét \(\Delta HDB\) vuông tại D có: \(\widehat {DBH} = \widehat {ABC} = {45^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BHD} = {90^0} - \widehat {DBH} = {90^0} - {45^0} = {45^0}\\ \Rightarrow \widehat {BHD} = \widehat {DBH} = {45^0}\end{array}\)
\( \Rightarrow \Delta HDB\)vuông cân tại D suy ra DB = DH (1)
Xét \(\Delta EGC\)vuông tại E có \(\widehat {ECG} = \widehat {BCA} = {45^0}\)
\(\begin{array}{l} \Rightarrow \widehat {CGE} = {90^0} - \widehat {ECG} = {90^0} - {45^0} = {45^0}\\ \Rightarrow \widehat {CGE} = \widehat {ECG} = {45^0}\end{array}\)
\( \Rightarrow \Delta EGC\)vuông cân tại E suy ra EC = EG (2)
Theo đề bài: BD = DE = EC (3)
Từ (1), (2), (3) suy ra: HD = DE =EG.
Xét tứ giác HDEG có HD//EG (vì cùng vuông góc với BC) HD = EG
Suy ra tứ giác HDEG là hình bình hành mà : \(\widehat {HDE} = {90^0}\)
Suy ra hình bình hành HDEG là hình chữ nhật.
Mặt khác: HD =DE. Suy ra hình chữ nhật HDEG là hình vuông
Video hướng dẫn giải
a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không?
b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 69)
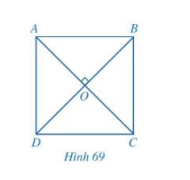
- Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
- ABCD có phải là hình vuông hay không?
c) Cho hình chữ nhật ABCD có AC là tia phân giác của góc DAB
- Tam giác ABC có phải là tam giác vuông cân hay không?
- ABCD có phải là hình vuông hay không?
Phương pháp giải:
Dựa vào tính chất của hình chữ nhật
Lời giải chi tiết:
a, Hình chữ nhật ABCD có AB = BC
Suy ra hình chữ nhật ABCD có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0};AB = BC = CD = DA\)
Suy ra hình chữ nhật ABCD là hình vuông
b, O là giao điểm của AC và BD.
Vì ABCD là hình chữ nhật nên OB = OD.
Mà AC vuông góc BD. Suy ra AC là đường trung trực của đoạn thẳng BD.
Xét \(\Delta ABD\) có AO vừa là đường trung trực vừa là đường cao
\( \Rightarrow \Delta ABD \) là tam giác vuông cân tại A.
\( \Rightarrow AB = AD\)
Mà AB = CD, AD = BC (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
c, Ta có ABCD là hình chữ nhật nên \(\widehat A =\widehat B = \widehat C = \widehat D = 90^0\)
Vì AC là tia phân giác của góc DAB nên ta có: \(\widehat{DAC} = \widehat{CAB} =\frac{\widehat{DAB}}{2} = \frac{90^0}{2} = 45^0\)
Xét tam giác ABC vuông tại B (\(\widehat B = 90^0\)), ta có:
\(\widehat{ACB} + \widehat B + \widehat{CAB} = 180^0\)
\(\Rightarrow \widehat{ACB} = 180^0 - \widehat B - \widehat{CAB} = 180^0 - 90^0 - 45^0 = 45^0\)
\( \Rightarrow \widehat{ACB} = \widehat{CAB} =45^0\) nên tam giác ABC vuông cân tại B.
\( \Rightarrow AB = BC\)
Mà AB = CD, BC = AD (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
Video hướng dẫn giải
a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không?
b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 69)
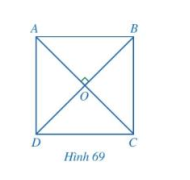
- Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
- ABCD có phải là hình vuông hay không?
c) Cho hình chữ nhật ABCD có AC là tia phân giác của góc DAB
- Tam giác ABC có phải là tam giác vuông cân hay không?
- ABCD có phải là hình vuông hay không?
Phương pháp giải:
Dựa vào tính chất của hình chữ nhật
Lời giải chi tiết:
a, Hình chữ nhật ABCD có AB = BC
Suy ra hình chữ nhật ABCD có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0};AB = BC = CD = DA\)
Suy ra hình chữ nhật ABCD là hình vuông
b, O là giao điểm của AC và BD.
Vì ABCD là hình chữ nhật nên OB = OD.
Mà AC vuông góc BD. Suy ra AC là đường trung trực của đoạn thẳng BD.
Xét \(\Delta ABD\) có AO vừa là đường trung trực vừa là đường cao
\( \Rightarrow \Delta ABD \) là tam giác vuông cân tại A.
\( \Rightarrow AB = AD\)
Mà AB = CD, AD = BC (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
c, Ta có ABCD là hình chữ nhật nên \(\widehat A =\widehat B = \widehat C = \widehat D = 90^0\)
Vì AC là tia phân giác của góc DAB nên ta có: \(\widehat{DAC} = \widehat{CAB} =\frac{\widehat{DAB}}{2} = \frac{90^0}{2} = 45^0\)
Xét tam giác ABC vuông tại B (\(\widehat B = 90^0\)), ta có:
\(\widehat{ACB} + \widehat B + \widehat{CAB} = 180^0\)
\(\Rightarrow \widehat{ACB} = 180^0 - \widehat B - \widehat{CAB} = 180^0 - 90^0 - 45^0 = 45^0\)
\( \Rightarrow \widehat{ACB} = \widehat{CAB} =45^0\) nên tam giác ABC vuông cân tại B.
\( \Rightarrow AB = BC\)
Mà AB = CD, BC = AD (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
Video hướng dẫn giải
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy điểm D, E sao cho: BD = DE = EC
Qua D và E kẻ đường thẳng vuông góc với BC, chúng cắt AB và AC lần lượt tại H và G. Chứng minh tứ giác DEGH là hình vuông.
Phương pháp giải:
Chứng minh tứ giác DEGH là hình chữ nhật có HD = DE
Lời giải chi tiết:
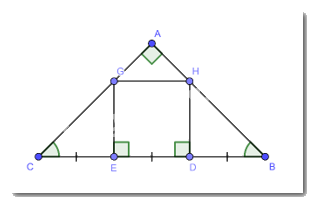
Xét \(\Delta ABC\) vuông cân tại A
\( \Rightarrow \widehat {ABC} = \widehat {ACB} = {45^0}\)
Xét \(\Delta HDB\) vuông tại D có: \(\widehat {DBH} = \widehat {ABC} = {45^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BHD} = {90^0} - \widehat {DBH} = {90^0} - {45^0} = {45^0}\\ \Rightarrow \widehat {BHD} = \widehat {DBH} = {45^0}\end{array}\)
\( \Rightarrow \Delta HDB\)vuông cân tại D suy ra DB = DH (1)
Xét \(\Delta EGC\)vuông tại E có \(\widehat {ECG} = \widehat {BCA} = {45^0}\)
\(\begin{array}{l} \Rightarrow \widehat {CGE} = {90^0} - \widehat {ECG} = {90^0} - {45^0} = {45^0}\\ \Rightarrow \widehat {CGE} = \widehat {ECG} = {45^0}\end{array}\)
\( \Rightarrow \Delta EGC\)vuông cân tại E suy ra EC = EG (2)
Theo đề bài: BD = DE = EC (3)
Từ (1), (2), (3) suy ra: HD = DE =EG.
Xét tứ giác HDEG có HD//EG (vì cùng vuông góc với BC) HD = EG
Suy ra tứ giác HDEG là hình bình hành mà : \(\widehat {HDE} = {90^0}\)
Suy ra hình bình hành HDEG là hình chữ nhật.
Mặt khác: HD =DE. Suy ra hình chữ nhật HDEG là hình vuông
Mục 3 trang 118 SGK Toán 8 tập 1 - Cánh diều thường xoay quanh các bài toán liên quan đến ứng dụng thực tế của phương trình bậc nhất một ẩn. Các bài toán này đòi hỏi học sinh phải nắm vững các bước giải phương trình, hiểu rõ ý nghĩa của ẩn số và biết cách biểu diễn các đại lượng trong bài toán bằng phương trình.
Để giải các bài tập trong Mục 3 trang 118 SGK Toán 8 tập 1 - Cánh diều một cách hiệu quả, các em cần thực hiện theo các bước sau:
Đề bài: Một ô tô đi từ A đến B với vận tốc 60km/h. Hỏi sau 2 giờ ô tô đi được bao nhiêu km?
Giải:
Gọi quãng đường ô tô đi được là x (km).
Ta có phương trình: x = 60 * 2
Giải phương trình, ta được: x = 120
Vậy sau 2 giờ ô tô đi được 120km.
Ngoài các bài toán về chuyển động, năng suất lao động và tỉ lệ, Mục 3 còn có thể xuất hiện các bài toán về tính phần trăm, lãi suất, và các bài toán kết hợp nhiều yếu tố. Để giải các bài toán này, các em cần linh hoạt vận dụng các kiến thức đã học và kết hợp với các kỹ năng tư duy logic.
Ngoài SGK Toán 8 tập 1 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Giải mục 3 trang 118 SGK Toán 8 tập 1 - Cánh diều đòi hỏi các em phải nắm vững kiến thức về phương trình bậc nhất một ẩn và các ứng dụng thực tế của nó. Bằng cách thực hành thường xuyên và áp dụng các phương pháp giải bài tập hiệu quả, các em sẽ tự tin giải quyết mọi bài toán toán học.