Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 1 trang 107, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán. Hãy cùng bắt đầu với bài 1 trang 107 nhé!
Cho tứ giác ABCD có
Đề bài
Cho tứ giác ABCD có \(\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {ABC} = \widehat {C{\rm{D}}A}\). Kẻ tia Ax là tia đối của tia AB. Chứng minh:
a) \(\widehat {ABC} + \widehat {DAB} = {180^o}\)
b) \(\widehat {xA{\rm{D}}} = \widehat {ABC};AC//BC\)
c) Tứ giác ABCD là hình bình hành.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng các góc của 1 tứ giác bằng \({360^0}.\)
Lời giải chi tiết
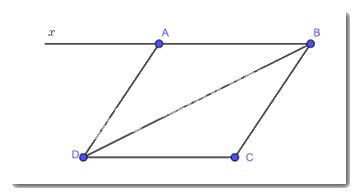
a, Tứ giác ABCD có:
\(\widehat {ABC} + \widehat {BCD} + \widehat {CDA} + \widehat {DAB} = {360^0}\)
\(\widehat {ABC} + \widehat {DAB} + \widehat {ABC} + \widehat {DAB} = {360^0}\)(do \(\widehat {DAB} = \widehat {BCD};\widehat {ABC} = \widehat {CDA}\))
\(\begin{array}{l}2\widehat {ABC} + 2\widehat {DAB} = {360^0}\\\widehat {ABC} + \widehat {DAB} = \dfrac{{{{360}^0}}}{2} = {180^0}\end{array}\)
b, Ta có: \(\widehat {xAD} + \widehat {DAB} = {180^0}\)(do tia Ax là tia đối của tia AB)
Nên \(\widehat {xAD} + \widehat {DAB} = \widehat {ABC} + \widehat {DAB}\)
Suy ra \( \widehat {xAD} = \widehat {ABC}\)
Suy ra AD//BC (hai góc đồng vị bằng nhau)
c, Vì AD//BC nên \(\widehat {ADB} = \widehat {DBC}\) (2 góc so le trong)
Xét \(\Delta ADB\) có \(\widehat {ABD} = {180^0} - \widehat {ADB} - \widehat {DAB} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 1 \right)\)
(vì \(\widehat {ADB} = \widehat {DBC};\widehat {DAB} = \widehat {BCD})\)
Xét \(\Delta CDB\) có: \(\widehat {BDC} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 2 \right)\)
Từ (1), (2) suy ra \(\widehat {ABD} =\widehat {BDC}\)
Xét \(\Delta ADB\) và \(\Delta BCD\) có:
\(\left. \begin{array}{l}DB \; chung\\\widehat {ABD} = \widehat {BDC}\\\widehat {BAD} = \widehat {DBC}\end{array} \right\}\)
Suy ra \(\Delta A{\rm{D}}B = \Delta C{\rm{D}}B\)
Do đó \(A{\rm{D}} = BC,AB = CB\)
Suy ra tứ giác ABCD có cặp cạnh đối bằng nhau nên ABCD là hình bình hành.
Bài 1 trang 107 SGK Toán 8 tập 1 - Cánh diều thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các kiến thức lý thuyết sau:
Ngoài ra, việc hiểu rõ các định lý và tính chất liên quan đến tam giác đồng dạng cũng rất quan trọng trong việc giải quyết các bài toán hình học nói chung và bài 1 trang 107 nói riêng.
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình thang cân ABCD có AB // CD, AD = BC. Gọi E là giao điểm của AC và BD. Chứng minh rằng: a) ΔADC = ΔBCD; b) EA = EB.)
Lời giải:
Xét ΔADC và ΔBCD, ta có:
Do đó, ΔADC = ΔBCD (c-g-c).
Vì ΔADC = ΔBCD (cmt) nên DC = DC (cạnh tương ứng).
Xét ΔAED và ΔBEC, ta có:
Do đó, ΔAED = ΔBEC (g-c-g).
Suy ra EA = EB (cạnh tương ứng).
Ngoài bài 1 trang 107, còn rất nhiều bài tập liên quan đến hình thang cân và các tứ giác đặc biệt khác. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn có thể tham khảo thêm các bài tập sau:
Hy vọng bài giải chi tiết bài 1 trang 107 SGK Toán 8 tập 1 - Cánh diều này đã giúp bạn hiểu rõ hơn về kiến thức và phương pháp giải các bài toán liên quan đến hình thang cân. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!