Chào mừng bạn đến với bài học về Lý thuyết Tam giác đồng dạng trong chương trình Toán 8 - Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về tam giác đồng dạng, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng ta sẽ cùng nhau khám phá các khái niệm, định nghĩa, tính chất và các trường hợp đồng dạng của tam giác. Đồng thời, bài học cũng sẽ cung cấp các ví dụ minh họa cụ thể để bạn dễ dàng hình dung và áp dụng vào thực tế.
Tam giác đồng dạng là gì?
1. Tam giác đồng dạng
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
\(\widehat {A'} = \widehat A,\widehat {B'} = \widehat B,\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\)
Kí hiệu: \(\Delta A'B'C' \backsim \Delta ABC\) (viết theo thứ tự cặp đỉnh tương ứng).
Tỉ số \(k = \frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) là tỉ số đồng dạng của \(\Delta A'B'C'\) với \(\Delta ABC\).
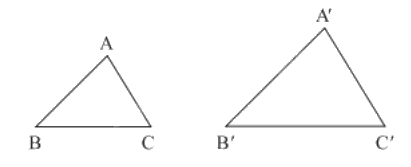
Nếu \(\Delta A'B'C' = \Delta ABC\) thì \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số đồng dạng là 1.
2. Tính chất
Tính chất 1. Mỗi tam giác đồng dạng với chính nó.
Tính chất 2. Nếu tam giác \(\Delta A''B''C'' \backsim \Delta A'B'C'\) và \(\Delta A'B'C' \backsim \Delta ABC\) thì \(\Delta A''B''C'' \backsim \Delta ABC\).
3. Định lí
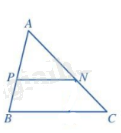
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
\(\begin{array}{l}\Delta ABC,PN//BC,P \in AB,N \in AC\\ \Rightarrow \Delta APN \backsim \Delta ABC\end{array}\)
Chú ý: Định lí trên cũng đúng trong trường hợp đường thẳng cắt phần kéo dài của hai cạnh của tam giác và song song với cạnh còn lại.
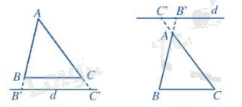
Tam giác đồng dạng là một khái niệm quan trọng trong hình học, đặc biệt là ở chương trình Toán 8. Hiểu rõ lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến tam giác, góc và tỉ lệ.
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Có ba trường hợp đồng dạng của tam giác:
Nếu hai tam giác đồng dạng, thì:
Tam giác đồng dạng có nhiều ứng dụng trong thực tế, ví dụ như:
Để hiểu rõ hơn về lý thuyết tam giác đồng dạng, chúng ta hãy xem xét một số bài tập vận dụng:
Bài tập 1: Cho tam giác ABC và tam giác A'B'C' có ∠A = ∠A', ∠B = ∠B'. Chứng minh rằng △ABC đồng dạng với △A'B'C'.
Bài tập 2: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm. Cho tam giác A'B'C' đồng dạng với tam giác ABC và có cạnh A'B' = 6cm. Tính độ dài các cạnh A'C' và B'C'.
Khi làm bài tập về tam giác đồng dạng, cần chú ý:
Lý thuyết Tam giác đồng dạng là một phần quan trọng của chương trình Toán 8. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.