Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 83 sách giáo khoa Toán 8 – Cánh diều. Bài viết này cung cấp đáp án chính xác, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và đầy đủ lời giải các bài tập trong SGK Toán 8 – Cánh diều, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
Cho hai tam giác ABC, A’B’C’ sao cho
Video hướng dẫn giải
Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\).
Phương pháp giải:
Tìm số đo các góc còn lại của hai tam giác rồi chứng minh \(\Delta ABC \backsim \Delta MNP\) theo trường hợp đồng dạng thứ ba.
Lời giải chi tiết:
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).
Video hướng dẫn giải
Cho hai tam giác ABC, A’B’C’ sao cho \(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\) và \(A'B' \ne AB\) (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn \(A'M = AB\). Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh \(\Delta A'MN = \Delta ABC\). Từ đó suy ra \(\Delta A'B'C' \backsim \Delta ABC\).
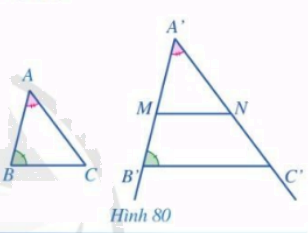
Phương pháp giải:
Chứng minh \(\Delta A'MN = \Delta ABC\) theo các trường hợp đã học từ đó chứng minh \(\Delta A'B'C' \backsim \Delta ABC\).
Lời giải chi tiết:
Vì \(MN\parallel B'C'\) nên \(\widehat {A'MN} = \widehat {A'B'C'}\) (hai góc đồng vị)
\( \Rightarrow \widehat M = \widehat B\)
Xét tam giác A’MN và tam giác ABC có:
\(\widehat {A'} = \widehat A;\,\,A'M = AB;\,\,\widehat M = \widehat B\)
\( \Rightarrow \Delta A'MN = \Delta ABC\) (g-c-g)
Vì \(MN\parallel B'C'\) nên \(\Delta A'MN \backsim \Delta A'B'C'\)
\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\)
Video hướng dẫn giải
Cho hai tam giác ABC, A’B’C’ sao cho \(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\) và \(A'B' \ne AB\) (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn \(A'M = AB\). Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh \(\Delta A'MN = \Delta ABC\). Từ đó suy ra \(\Delta A'B'C' \backsim \Delta ABC\).
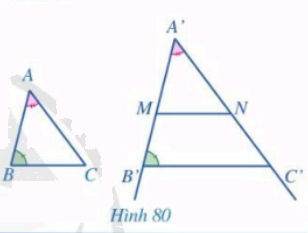
Phương pháp giải:
Chứng minh \(\Delta A'MN = \Delta ABC\) theo các trường hợp đã học từ đó chứng minh \(\Delta A'B'C' \backsim \Delta ABC\).
Lời giải chi tiết:
Vì \(MN\parallel B'C'\) nên \(\widehat {A'MN} = \widehat {A'B'C'}\) (hai góc đồng vị)
\( \Rightarrow \widehat M = \widehat B\)
Xét tam giác A’MN và tam giác ABC có:
\(\widehat {A'} = \widehat A;\,\,A'M = AB;\,\,\widehat M = \widehat B\)
\( \Rightarrow \Delta A'MN = \Delta ABC\) (g-c-g)
Vì \(MN\parallel B'C'\) nên \(\Delta A'MN \backsim \Delta A'B'C'\)
\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\)
Video hướng dẫn giải
Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\).
Phương pháp giải:
Tìm số đo các góc còn lại của hai tam giác rồi chứng minh \(\Delta ABC \backsim \Delta MNP\) theo trường hợp đồng dạng thứ ba.
Lời giải chi tiết:
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).
Mục 1 trang 83 SGK Toán 8 – Cánh diều thường xoay quanh các bài tập về ứng dụng của phương pháp cộng, trừ, nhân, chia đa thức. Để giải quyết hiệu quả các bài toán này, học sinh cần nắm vững các kiến thức cơ bản về đa thức, các phép toán trên đa thức và các quy tắc biến đổi đại số.
Mục 1 thường bao gồm các dạng bài tập sau:
Để giải các bài tập trong Mục 1 trang 83, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Tính giá trị của biểu thức A = 2x2 + 3x - 1 tại x = -1.
Giải: Thay x = -1 vào biểu thức A, ta được:
A = 2(-1)2 + 3(-1) - 1 = 2(1) - 3 - 1 = 2 - 3 - 1 = -2.
Ví dụ: Rút gọn biểu thức B = (x + 2)(x - 2) + x2.
Giải: Sử dụng hằng đẳng thức (a + b)(a - b) = a2 - b2, ta có:
B = x2 - 4 + x2 = 2x2 - 4.
Ví dụ: Tìm nghiệm của đa thức C = x2 - 4.
Giải: Đặt C = 0, ta có:
x2 - 4 = 0 ⇔ x2 = 4 ⇔ x = ±2.
Vậy, đa thức C có hai nghiệm là x = 2 và x = -2.
Ví dụ: Giải phương trình 2x + 4 = 0.
Giải: Chuyển vế và rút gọn, ta có:
2x = -4 ⇔ x = -2.
Vậy, phương trình có nghiệm là x = -2.
Ngoài SGK Toán 8 – Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Mục 1 trang 83 SGK Toán 8 – Cánh diều. Chúc các em học tập tốt!