Phương trình bậc nhất một ẩn là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 8, sách Cánh diều. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết Phương trình bậc nhất một ẩn, cùng với các bài tập vận dụng đa dạng để giúp bạn học tập hiệu quả.
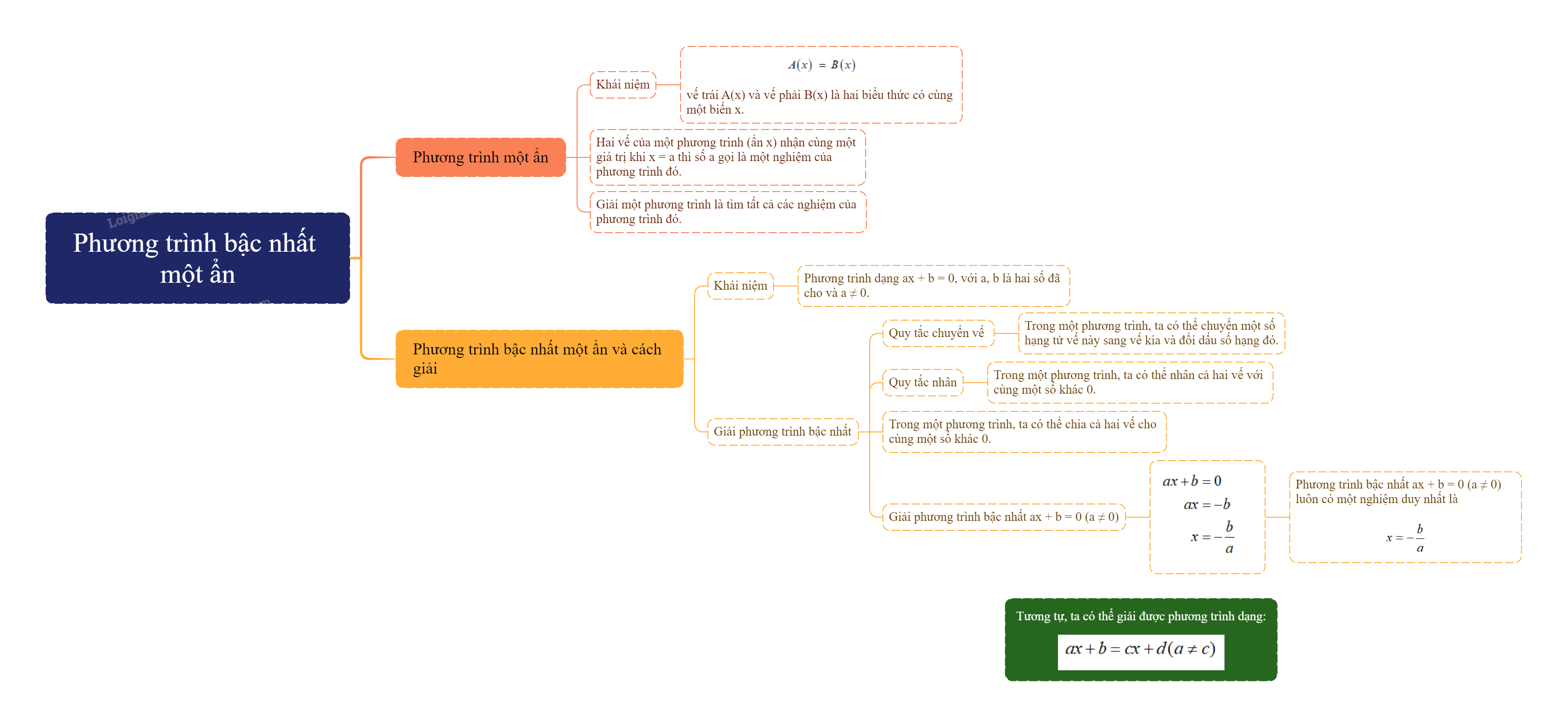
Phương trình bậc nhất một ẩn là gì
1. Khái niệm:
Một phương trình với ẩn x có dạng \(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức có cùng một biến x.
Ví dụ: \(3x-1 = 2x + 3;3x = 5\) là các phương trình ẩn x.
Nếu hai vế của một phương trình (ẩn x) nhận cùng một giá trị khi x = a thì số a gọi là một nghiệm của phương trình đó.
Ví dụ: \(x = 2\) là nghiệm của phương trình \(2x = x + 2\) vì thay \(x = 2\) vào phương trình, ta được 2.2 = 2 + 2
Khi bài toán yêu cầu giải một phương trình, ta phải tìm tất cả các nghiệm của phương trình đó.
Ví dụ: Giải phương trình: \(3x + 6 = 0\)
Ta có: \(3x + 6 = 0 \Leftrightarrow 3x = - 6 \Leftrightarrow x = - 2\)
Vậy tập nghiệm của phương trình là S = {-2}
2. Phương trình bậc nhất một ẩn và cách giải
Khái niệm: Phương trình dạng ax + b = 0, với a, b là hai số đã cho và \(a \ne 0\), được gọi là phương trình bậc nhất một ẩn.
Cách giải:
Đối với phương trình, ta cũng có quy tắc chuyển vế như sau: Trong một phương trình, ta có thể chuyển một số hạng tử vế này sang vế kia và đổi dấu số hạng đó.
Đối với phương trình, ta cũng có quy tắc nhân với một số ( gọi tắt là quy tắc nhân) như sau: Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.
Tương tự, Trong một phương trình, ta có thể chia cả hai vế cho cùng một số khác 0.
Phương trình bậc nhất ax + b = 0 (\(a \ne 0\)) được giải như sau:
\(\begin{array}{c}ax + b = 0\\ax = - b\\x = - \frac{b}{a}\end{array}\)
Phương trình bậc nhất ax + b = 0 (\(a \ne 0\)) luôn có một nghiệm duy nhất là \(x = - \frac{b}{a}\).
Ví dụ: Giải phương trình: \(3x + 11 = 0\)
Ta có: \(3x + 11 = 0 \Leftrightarrow 3x = - 11 \Leftrightarrow x = - \frac{{11}}{3}\)
Vậy nghiệm của phương trình là \(x = - \frac{{11}}{3}\).
Nhận xét: Bằng cách tương tự như trên, ta có thể giải được phương trình dạng:
\(ax + b = cx + d(a \ne c)\)
Ví dụ: Giải phương trình: \(7x-\left( {2x + 3} \right) = 5\left( {x-2} \right)\)
\(\begin{array}{c}11x-\left( {2x + 3} \right) = {\rm{ 6}}\left( {x-2} \right)\\11x - 2x - 3 = 6x - 12\\11x - 2x - 6x = - 12 + 3\\3x = - 9\\x = \frac{{ - 9}}{3}\\x = - 3\end{array}\)
Vậy nghiệm của phương trình là x = -3
Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0, trong đó x là ẩn số, a và b là các hệ số với a ≠ 0. Hiểu rõ định nghĩa này là bước đầu tiên để làm chủ chủ đề này.
Như đã đề cập, phương trình bậc nhất một ẩn có dạng tổng quát là ax + b = 0 (với a ≠ 0). Ẩn số là đại lượng chưa biết, cần tìm giá trị để thỏa mãn phương trình. Hệ số a xác định bậc của phương trình (trong trường hợp này là bậc nhất). Hệ số b là hằng số.
Để giải phương trình bậc nhất một ẩn, chúng ta thực hiện các bước sau:
Ví dụ 1: Giải phương trình 2x + 5 = 11
Vậy nghiệm của phương trình là x = 3.
Ví dụ 2: Giải phương trình -3x - 7 = 8
Vậy nghiệm của phương trình là x = -5.
Trong SGK Toán 8 Cánh diều, các bài tập về phương trình bậc nhất một ẩn thường gặp các dạng sau:
Để giải nhanh các bài tập về phương trình bậc nhất một ẩn, bạn nên:
Kiến thức về phương trình bậc nhất một ẩn có liên hệ mật thiết với các kiến thức khác trong chương trình Toán 8, như:
Để củng cố kiến thức về phương trình bậc nhất một ẩn, bạn nên làm thêm các bài tập trong sách bài tập, trên các trang web học toán online như giaitoan.edu.vn, hoặc tham gia các khóa học luyện thi Toán.
Việc hiểu rõ và nắm vững lý thuyết Phương trình bậc nhất một ẩn là bước đệm quan trọng để bạn học tốt môn Toán 8 và chuẩn bị cho các kiến thức nâng cao hơn trong tương lai. Chúc bạn học tập hiệu quả!