Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 3 trang 100, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán. Hãy cùng bắt đầu với bài 3 trang 100 SGK Toán 8 tập 1 - Cánh diều ngay bây giờ!
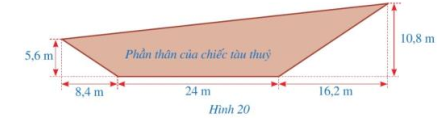
Hình 20 mô tả mặt cắt dọc phần nổi trên mặt nước của một chiếc tàu thủy.
Đề bài
Một chiếc tàu thủy có mặt cắt dọc phần nổi trên mặt nước của tân tàu được mô tả ở Hình 20. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của thân tàu đó (làm tròn kết quả đến hàng phần mười của mét).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Ta đánh dấu các điểm của các tam giác vuông
Áp dụng định lí Pythagore để tính độ dài các cạnh.
Lời giải chi tiết
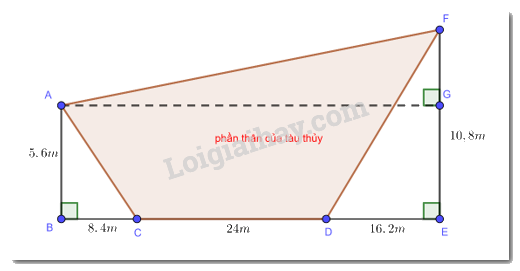
*) Áp dụng định lí Pythagore trong tam giác \(\Delta ABC\) vuông tại A có
\(A{C^2} = A{B^2} + B{C^2} = 5,{6^2} + 8,{4^2} = 101,92 \Rightarrow AC = \sqrt {101,92} \)
\(\Delta DEF\) vuông tại F có
\(D{F^2} = D{E^2} + E{F^2} = 16,{2^2} + 10,{8^2} = 379,08 \Rightarrow DF = \sqrt {379,08} \)
Kẻ \(AG \bot FG\)
Khi đó: \(FG = FE - GE = FE - AB = 10,8 - 5,6 = 5,2\)
Áp dụng định lí Pythagore trong \(\Delta AGF\) vuông tại G có
\(A{F^2} = A{G^2} + F{G^2} = 48,{6^2} + 5,{2^2} = 2389 \Rightarrow AF = \sqrt {2389} \)
Chu vi tứ giác ACDF là:
\(AC + CD + DF + AF = \sqrt {101,92} + \sqrt {379,08} + 24 + \sqrt {2389} \approx 102,4\)
Vậy chu vi của mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thủy là khoảng 102,4m.
Bài 3 trang 100 SGK Toán 8 tập 1 - Cánh diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Bài 3 yêu cầu học sinh chứng minh một số tính chất liên quan đến các đường chéo của các hình đặc biệt. Cụ thể, bài tập thường xoay quanh việc chứng minh các đường chéo của hình chữ nhật cắt nhau tại trung điểm của mỗi đường, các đường chéo của hình thoi vuông góc với nhau, và các đường chéo của hình vuông vừa vuông góc vừa cắt nhau tại trung điểm của mỗi đường.
Để giải quyết bài toán này, học sinh có thể áp dụng các phương pháp sau:
Bài 3: (Cánh diều) Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng OA = OB = OC = OD.
Lời giải:
Để hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ minh họa:
Ví dụ: Cho hình thoi ABCD có AC và BD cắt nhau tại O. Chứng minh rằng AC vuông góc với BD.
Lời giải:
Vì ABCD là hình thoi nên AC và BD vuông góc với nhau (tính chất hình thoi). Do đó, góc AOB = 90 độ.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 3 trang 100 SGK Toán 8 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các tính chất của các hình đặc biệt. Bằng cách nắm vững lý thuyết và áp dụng các phương pháp giải phù hợp, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả. Chúc bạn học tập tốt!
| Hình | Tính chất |
|---|---|
| Hình bình hành | Các cạnh đối song song và bằng nhau; Các góc đối bằng nhau; Hai đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình chữ nhật | Có bốn góc vuông; Các cạnh đối song song và bằng nhau; Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường. |
| Hình thoi | Bốn cạnh bằng nhau; Các cạnh đối song song; Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. |
| Hình vuông | Có bốn góc vuông và bốn cạnh bằng nhau; Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. |