Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 79 SGK Toán 8 tập 1 - Cánh diều. Bài học này thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
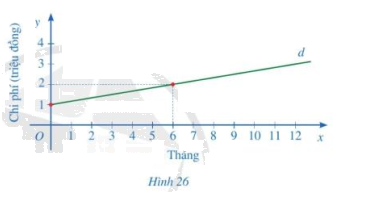
Để sử dụng dịch vụ truyền hình cáp,
Đề bài
Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hằng tháng. Một phần đường thẳng d ở hình 26 biểu thị tổng chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng d.
b) Giao điểm của đường thẳng d với trục tung trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi hàm số bậc nhất là y = ax + b (a\( \ne \)0)
Quan sát hình 26 để xác định a, b
Lời giải chi tiết
a) Gọi hàm số bậc nhất của đường thẳng d là y = ax + b (a\( \ne \)0)
Từ hình 26, ta thấy đường thẳng d đi qua hai điểm (0; 1) và (6; 2)
Thay tọa độ điểm (0; 1) vào hàm số y = ax + b ta được:
1 = a. 0 + b suy ra b = 1
Hàm số bậc nhất là y = ax + 1 (a\( \ne \)0) (1)
Vì đường thẳng d đi qua điểm (6; 2) nên thay tọa độ điểm (6; 2) vào hàm số (1) ta được là:
2 = a. 6 + 1 suy ra \(a = \dfrac{1}{6}\)
Vậy hàm số của đường thẳng d là \(y = \dfrac{1}{6}x + 1\)
b) Giao điểm của đường thẳng d với trục tung là 1 trong tình huống này có nghĩa là người dùng phải trả khoản phí bạn đầu là 1 triệu đồng
c) Tổng chi phí mà gia đình phải trả khi sử dụng dịch vụ truyền hình với thời gian 12 tháng là ta thay x = 12 vào hàm số \(y = \dfrac{1}{6}x + 1\)
Khi đó: \(y = \dfrac{1}{6}.12 + 1 = 3\)
Tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là 3 triệu đồng.
Bài 7 trang 79 SGK Toán 8 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số để giải quyết các bài toán liên quan đến biểu thức đại số. Để làm tốt bài tập này, các em cần nắm vững các khái niệm cơ bản như đơn thức, đa thức, cộng, trừ, nhân, chia đa thức, và các hằng đẳng thức đáng nhớ.
Bài 7 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh thực hiện các thao tác sau:
Để giải câu a, ta cần phân tích đa thức thành nhân tử. Sử dụng các hằng đẳng thức đáng nhớ, ta có thể viết lại đa thức dưới dạng tích của các nhân tử. Sau đó, ta có thể đơn giản hóa biểu thức bằng cách loại bỏ các nhân tử chung.
Câu b yêu cầu ta rút gọn biểu thức đại số. Để làm điều này, ta cần thực hiện các phép toán cộng, trừ, nhân, chia đa thức theo đúng thứ tự ưu tiên. Lưu ý sử dụng các quy tắc dấu và các hằng đẳng thức để đơn giản hóa biểu thức.
Câu c yêu cầu ta tìm giá trị của biểu thức khi biết giá trị của các biến. Ta chỉ cần thay thế các giá trị của biến vào biểu thức và thực hiện các phép toán để tính ra kết quả.
Câu d là một bài toán giải phương trình. Để giải phương trình, ta cần thực hiện các phép biến đổi đại số để đưa phương trình về dạng đơn giản nhất. Sau đó, ta có thể tìm ra giá trị của biến bằng cách chia cả hai vế của phương trình cho hệ số của biến.
Ví dụ 1: Phân tích đa thức x2 - 4 thành nhân tử.
Giải: Ta có x2 - 4 = (x - 2)(x + 2)
Ví dụ 2: Rút gọn biểu thức 2x + 3x - 5x.
Giải: Ta có 2x + 3x - 5x = (2 + 3 - 5)x = 0x = 0
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể tự giải các bài tập tương tự trong SGK và các tài liệu tham khảo khác.
Bài 7 trang 79 SGK Toán 8 tập 1 - Cánh diều là một bài tập quan trọng giúp các em rèn luyện kỹ năng giải các bài toán đại số cơ bản. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin giải quyết bài tập một cách hiệu quả.