Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 3 trang 106, 107 sách giáo khoa Toán 8 tập 1 chương trình Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
a) Cho tứ giác ABCD có AB = CD, BC = DA (hình 39) - Hai tam giác ABC và CDA có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: (widehat {BAC}) và (widehat {DCA};widehat {ACB}) và (widehat {C{rm{D}}A}). ABCD có phải là hình bình hành hay không?
Video hướng dẫn giải
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn: OA = OC và \(\widehat {OA{\rm{D}}} = \widehat {OCB}\). Chứng minh tứ giác ABCD là hình bình hành.
Phương pháp giải:
Chứng minh tứ giác ABCD có: OA = OC; OB = OD
Lời giải chi tiết:
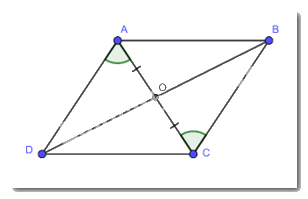
Xét tam giác AOD và tam giác COB có:
\(\begin{array}{l}OA = OC\\\widehat {DAO} = \widehat {BCO}(gt)\\\widehat {AO{\rm{D}}} = \widehat {BOC}(gt)\\ \Rightarrow \Delta AO{\rm{D}} = \Delta COB\\ \Rightarrow O{\rm{D}} = OB\end{array}\)
Tứ giác ABCD có OA = OC; OB = OD nên tứ giác ABCD là hình bình hành.
Video hướng dẫn giải
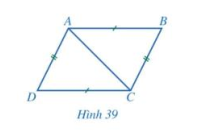
a) Cho tứ giác ABCD có AB = CD, BC = DA (hình 39)
- Hai tam giác ABC và CDA có bằng nhau hay không?
Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CAD}\).
ABCD có phải là hình bình hành hay không?
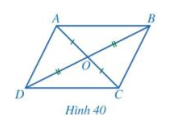
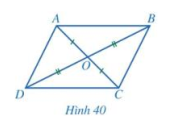
b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40)
Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CA{\rm{D}}}\).
ABCD có phải là hình bình hành hay không?
Phương pháp giải:
Chứng minh các tam giác bằng nhau từ đo suy ra các cạnh và các góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác ABC và CDA có:AB = CD; AD = BC; AC chung nên \(\Delta ABC = \Delta C{\rm{D}}A(c - c - c)\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CAD}\).
Nên ABCD hình bình hành.
b) Xét hai tam giác ABO và tam giác CDO có: \(OA = OB;\widehat {AOB} = \widehat {CO{\rm{D}}};OC = O{\rm{D}}\)
Suy ra: \(\Delta ABO = \Delta C{\rm{D}}O\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CA{\rm{D}}}\).
Nên ABCD là hình bình hành.
Video hướng dẫn giải
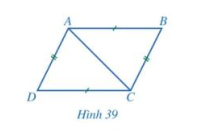
a) Cho tứ giác ABCD có AB = CD, BC = DA (hình 39)
- Hai tam giác ABC và CDA có bằng nhau hay không?
Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CAD}\).
ABCD có phải là hình bình hành hay không?
b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40)
Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CA{\rm{D}}}\).
ABCD có phải là hình bình hành hay không?
Phương pháp giải:
Chứng minh các tam giác bằng nhau từ đo suy ra các cạnh và các góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác ABC và CDA có:AB = CD; AD = BC; AC chung nên \(\Delta ABC = \Delta C{\rm{D}}A(c - c - c)\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CAD}\).
Nên ABCD hình bình hành.
b) Xét hai tam giác ABO và tam giác CDO có: \(OA = OB;\widehat {AOB} = \widehat {CO{\rm{D}}};OC = O{\rm{D}}\)
Suy ra: \(\Delta ABO = \Delta C{\rm{D}}O\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CA{\rm{D}}}\).
Nên ABCD là hình bình hành.
Video hướng dẫn giải
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn: OA = OC và \(\widehat {OA{\rm{D}}} = \widehat {OCB}\). Chứng minh tứ giác ABCD là hình bình hành.
Phương pháp giải:
Chứng minh tứ giác ABCD có: OA = OC; OB = OD
Lời giải chi tiết:
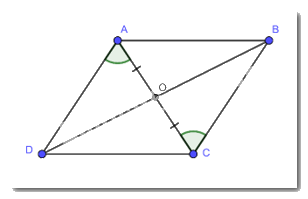
Xét tam giác AOD và tam giác COB có:
\(\begin{array}{l}OA = OC\\\widehat {DAO} = \widehat {BCO}(gt)\\\widehat {AO{\rm{D}}} = \widehat {BOC}(gt)\\ \Rightarrow \Delta AO{\rm{D}} = \Delta COB\\ \Rightarrow O{\rm{D}} = OB\end{array}\)
Tứ giác ABCD có OA = OC; OB = OD nên tứ giác ABCD là hình bình hành.
Mục 3 trong SGK Toán 8 tập 1 - Cánh diều thường tập trung vào một chủ đề cụ thể, ví dụ như các phép biến đổi đại số, giải phương trình bậc nhất một ẩn, hoặc các bài toán liên quan đến tam giác. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập trong mục này.
Để hiểu rõ hơn về Mục 3, chúng ta cần xác định chính xác nội dung mà nó đề cập đến. Thông thường, sách giáo khoa sẽ trình bày các kiến thức cơ bản, ví dụ minh họa và sau đó là các bài tập vận dụng. Các em học sinh cần đọc kỹ lý thuyết, hiểu rõ các ví dụ và ghi chép lại những điểm quan trọng.
Tùy thuộc vào nội dung cụ thể của Mục 3, phương pháp giải bài tập sẽ khác nhau. Tuy nhiên, có một số phương pháp chung mà các em có thể áp dụng:
Đề bài: (Giả định một đề bài cụ thể ở đây, ví dụ: Rút gọn biểu thức: 2x + 3y - x + y)
Lời giải:
2x + 3y - x + y = (2x - x) + (3y + y) = x + 4y
Vậy, kết quả của biểu thức là x + 4y.
Đề bài: (Giả định một đề bài cụ thể ở đây, ví dụ: Tìm x biết: 3x - 5 = 7)
Lời giải:
3x - 5 = 7
3x = 7 + 5
3x = 12
x = 12 / 3
x = 4
Vậy, x = 4.
Đề bài: (Giả định một đề bài cụ thể ở đây, ví dụ: Cho tam giác ABC, biết góc A = 60 độ, góc B = 80 độ. Tính góc C.)
Lời giải:
Trong tam giác ABC, ta có:
Góc A + góc B + góc C = 180 độ
60 độ + 80 độ + góc C = 180 độ
140 độ + góc C = 180 độ
Góc C = 180 độ - 140 độ
Góc C = 40 độ
Vậy, góc C = 40 độ.
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 8. Chúc các em học tốt!