Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 85 SGK Toán 8 – Cánh diều. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
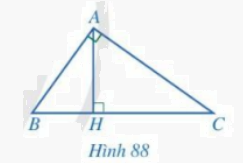
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:
Đề bài
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:
a) \(\Delta ABC \backsim \Delta HBA\) và \(A{B^2} = BC.BH\)
b) \(\Delta ABC \backsim \Delta HAC\) và \(A{C^2} = BC.CH\)
c) \(\Delta ABH \backsim \Delta CAH\) và \(A{H^2} = BH.CH\)
d) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh các cặp tam giác đồng dạng rồi suy ra tỉ số đồng dạng tương ứng.
Lời giải chi tiết

a) Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {BHA} = 90^\circ ;\,\,\widehat B\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g)
\( \Rightarrow \frac{{AB}}{{HB}} = \frac{{BC}}{{BA}} \Rightarrow A{B^2} = BC.HB\)
b) Xét tam giác ABC và tam giác HAC có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ ;\,\,\widehat C\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HAC\) (g-g)
\( \Rightarrow \frac{{AC}}{{HC}} = \frac{{BC}}{{AC}} \Rightarrow A{C^2} = BC.CH\)
c) Ta có: \(\Delta ABC \backsim \Delta HBA\) và \(\Delta ABC \backsim \Delta HAC\) nên \(\Delta ABH \backsim \Delta CAH\)
\( \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}} \Rightarrow A{H^2} = BH.CH\)
d) Ta có:
\(A{B^2} = BC.BH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.BH}}\)
\(A{C^2} = BC.CH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.CH}}\)
\(A{H^2} = BH.CH \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{BH.CH}}\)
\(\begin{array}{l} \Rightarrow \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{BC.BH}} + \frac{1}{{BC.CH}}\\ = \frac{1}{{BC}}.\left( {\frac{1}{{BH}} + \frac{1}{{CH}}} \right)\\ = \frac{1}{{BC}}.\frac{{BH + CH}}{{BH.CH}}\\ = \frac{1}{{BC}}.\frac{{BC}}{{BH.CH}}\\ = \frac{1}{{BH.CH}}\\ = \frac{1}{{A{H^2}}}\end{array}\)
Bài 5 trang 85 SGK Toán 8 – Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về các hình khối, đặc biệt là hình hộp chữ nhật và hình lập phương. Bài tập này không chỉ giúp củng cố lý thuyết mà còn rèn luyện kỹ năng giải toán không gian, một kỹ năng cần thiết cho các bài học nâng cao hơn.
Bài 5 trang 85 SGK Toán 8 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các công thức sau:
Ngoài ra, học sinh cần đọc kỹ đề bài, xác định đúng các yếu tố đã cho và yêu cầu của bài toán. Vẽ hình minh họa có thể giúp học sinh hình dung rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
Ví dụ 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính thể tích của hình hộp chữ nhật đó.
Giải:
Thể tích của hình hộp chữ nhật là: V = 5 * 3 * 4 = 60 cm3
Ví dụ 2: Một hình lập phương có cạnh 6cm. Tính diện tích bề mặt của hình lập phương đó.
Giải:
Diện tích bề mặt của hình lập phương là: S = 6 * 62 = 216 cm2
Khi giải bài tập về hình hộp chữ nhật và hình lập phương, học sinh cần chú ý các điểm sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tự giải các bài tập sau:
Bài 5 trang 85 SGK Toán 8 – Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình hộp chữ nhật và hình lập phương. Bằng cách nắm vững các công thức, phương pháp giải và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài tập và đạt kết quả tốt trong học tập.