Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 104 SGK Toán 8 tập 1 - Cánh diều. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.
Đề bài
Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh BKEC là hình thang có \(\widehat {ABC} = \widehat {ACB}\)
Lời giải chi tiết
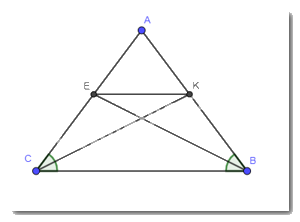
Do BE là phân giác của \(\widehat {ABC}\)nên \[\widehat {{B_1}} = \widehat {{B_2}} = \frac{{\widehat {ABC}}}{2}\]
CK là phân giác của \(\widehat {ACB}\) nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat {ACB}}}{2}\)
Mà: \(\widehat {ABC} = \widehat {ACB} = \frac{{{{180}^0} - \widehat A}}{2}(1)\)(do \(\Delta ABC\)cân tại A)
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
Xét \(\Delta AEB\)và \(\Delta AKC\)có: \(\widehat A\)chung, \(\widehat {{B_1}} = \widehat {{C_1}}\)
AB = AC \( \Rightarrow \Delta AEB = \Delta AKC(g.c.g)\)
\( \Rightarrow AE = AK \Rightarrow \Delta AEK\)cân tại A.. \(\widehat {AEK} = \widehat {AKE} = \frac{{{{180}^0} - \widehat A}}{2}(2)\)
Từ (1), (2) suy ra: \(\widehat {ABC} = \widehat {AKE} \Rightarrow KE//BC\)(2 góc đồng vị)
Suy ra BKEC là hình thang (3)
Từ (1), (3) suy ra BKEC là hình thang cân.
Bài 4 trang 104 SGK Toán 8 tập 1 - Cánh diều thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Bài toán này yêu cầu học sinh phải hiểu rõ các tính chất của hình chữ nhật, đặc biệt là mối quan hệ giữa các cạnh đối và các góc đối.
Bài 4 yêu cầu học sinh chứng minh một tính chất liên quan đến hình chữ nhật. Cụ thể, bài toán thường đưa ra một hình chữ nhật ABCD và yêu cầu chứng minh một đẳng thức hoặc một mối quan hệ giữa các đoạn thẳng hoặc các góc trong hình.
Để giải bài 4 trang 104 SGK Toán 8 tập 1 - Cánh diều, học sinh cần áp dụng các kiến thức và kỹ năng sau:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét cụ thể nội dung của bài toán. Giả sử bài toán yêu cầu chứng minh rằng đường chéo AC của hình chữ nhật ABCD chia đôi góc BAD. Lời giải sẽ như sau:
Chứng minh:
Để hiểu rõ hơn về phương pháp giải, chúng ta hãy xem xét một ví dụ minh họa khác. Giả sử bài toán yêu cầu chứng minh rằng giao điểm của hai đường chéo của hình chữ nhật ABCD là trung điểm của mỗi đường chéo.
Chứng minh:
Để củng cố kiến thức và kỹ năng giải bài tập về hình chữ nhật, học sinh có thể luyện tập thêm các bài tập sau:
Bài 4 trang 104 SGK Toán 8 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các tính chất của hình chữ nhật và rèn luyện kỹ năng giải toán hình học. Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, học sinh sẽ tự tin hơn khi làm bài tập về nhà và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục kiến thức Toán học. Chúc các em học tập tốt!