Chào mừng bạn đến với bài học lý thuyết về các phép tính với đa thức nhiều biến, một phần quan trọng trong chương trình Toán 8 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để hiểu rõ về cấu trúc, tính chất và các phép toán trên đa thức nhiều biến.
Chúng ta sẽ cùng nhau khám phá các khái niệm như biến, bậc của đa thức, các phép cộng, trừ, nhân, chia đa thức nhiều biến, cùng với các ví dụ minh họa cụ thể để bạn dễ dàng nắm bắt kiến thức.
Cộng hai đa thức nhiều biến như thế nào?
1. Cộng hai đa thức nhiều biến
Để cộng hai đa thức theo hàng ngang, ta có thể làm như sau:
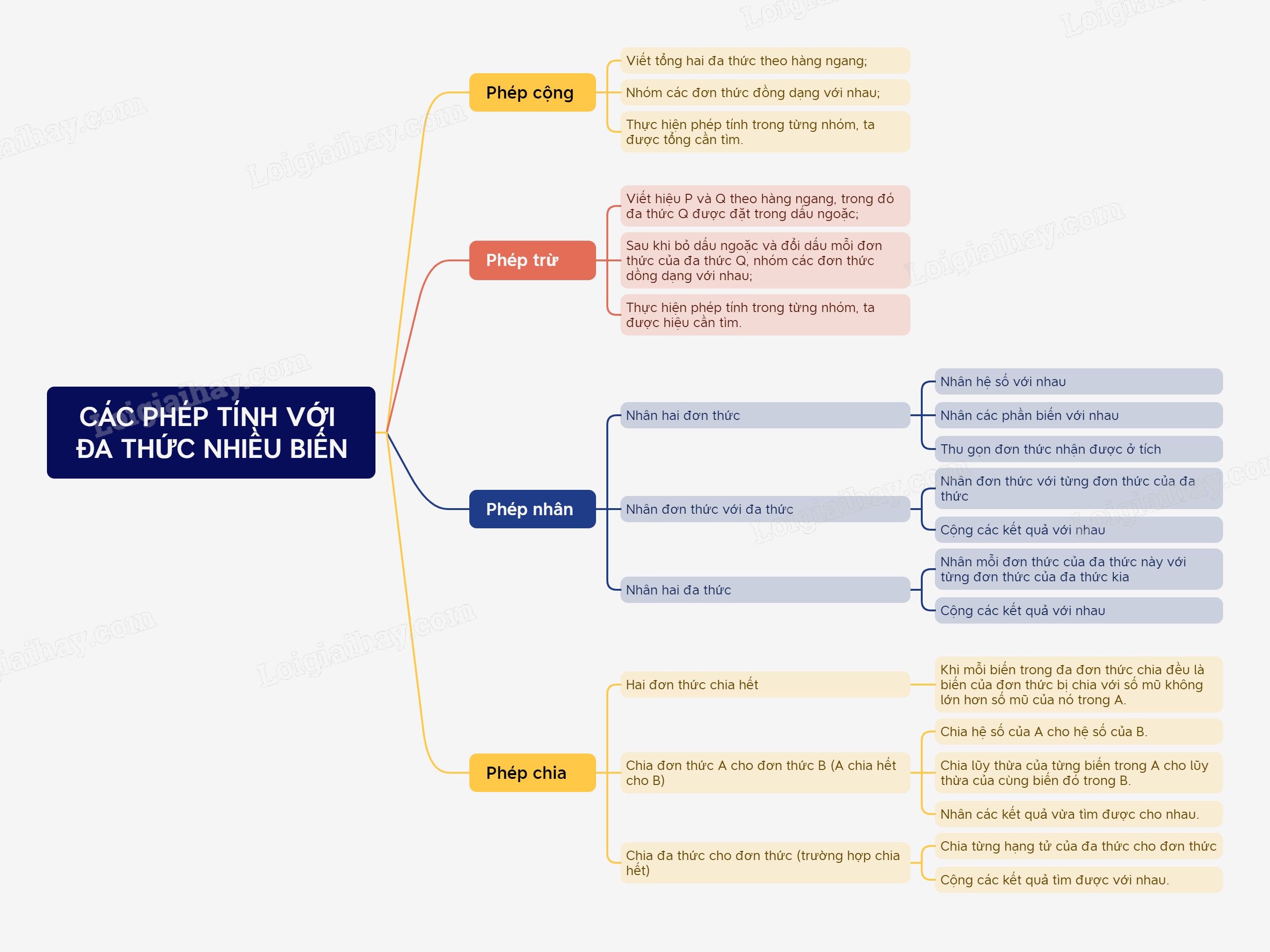
- Viết tổng hai đa thức theo hàng ngang;
- Nhóm các đơn thức đồng dạng với nhau;
- Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
2. Trừ hai đa thức nhiềm biến
Để trừ đa thức P cho đa thức Q theo hàng ngang, ta có thể làm như sau:
- Viết hiệu P và Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc;
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q, nhóm các đơn thức dồng dạng với nhau;
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Ví dụ:
Cho hai đa thức \(A = 3{x^2} - xy\)và \(B = {x^2} + 2xy - {y^2}\)
\(\begin{array}{l}A + B = \left( {3{x^2} - xy} \right) + \left( {{x^2} + 2xy - {y^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - xy + {x^2} + 2xy - {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = (3{x^2} + {x^2}) + ( - xy + 2xy) - {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 4{x^2} + xy - {y^2}\end{array}\)
\(\begin{array}{l}A - B = \left( {3{x^2} - xy} \right) - \left( {{x^2} + 2xy - {y^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - xy - {x^2} - 2xy + {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = (3{x^2} - {x^2}) + ( - xy - 2xy) + {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 2{x^2} - 3xy + {y^2}\end{array}\)
3. Nhân đa thức
Nhân hai đơn thức
Để nhân hai đơn thức, ta nhân các hệ số với nhau, nhân các phần biến với nhau; thu gọn đơn thức nhận được ở tích.
Ví dụ: \(( - 3{x^2}y)(4xy) = \left[ {\left( { - 3.4} \right)} \right].({x^2}.x).\left( {y.y} \right) = - 12.{x^3}.{y^2}\)
Nhân đơn thức với đa thức
Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng đơn thức của đa thức, rồi cộng các kết quả với nhau.
Ví dụ:
\(\begin{array}{l}3{x^2}y\left( {2{x^2}y - xy + 3{y^2}} \right)\\ = (3{x^2}y).(2{x^2}y) - (3{x^2}y).(xy) + (3{x^2}y).(3{y^2})\\ = 3.2.({x^2}.{x^2})\left( {y.y} \right) - 3.({x^2}.x).\left( {y.y} \right) + 3.3.{x^2}.\left( {y.{y^2}} \right)\\ = 6{x^4}{y^2} - 3{x^3}.{y^2} + 9{x^2}{y^3}\end{array}\)
Nhân hai đa thức
Để nhân hai đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia, rồi cộng các kết quả với nhau.
Ví dụ:
\(\begin{array}{l}(xy + 1)(xy - 3)\\ = (xy).\left( {xy} \right) + xy - 3xy - 3\\ = {x^2}{y^2} - 2xy - 3\end{array}\)
4. Chia đa thức cho đơn thức
Hai đơn thức chia hết cho nhau
Đơn thức A chia hết cho đơn thức B (\(B \ne 0\)) khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Chia đa thức cho đơn thức
Muốn chia đơn thức A cho đơn thức B (với A chia hết cho B), ta làm như sau:
- Chia hệ số của A cho hệ số của B.
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được cho nhau.
Ví dụ:
\(\begin{array}{l}16{x^4}{y^3}:( - 8{x^3}{y^2})\\ = (16:( - 8)).({x^4}:{x^3}).\left( {{y^3}:{y^2}} \right)\\ = - 2xy\end{array}\)
Đa thức chia hết cho đơn thức
Đa thức A chia hết cho B (\(B \ne 0\)) khi mỗi đơn thức của A chia hết cho B.
Chia đa thức cho đơn thức
Muốn chia một đa thức cho một đơn thức (trường hợp chia hết), ta chia từng hạng tử của đa thức cho đơn thức đó, rồi cộng các kết quả tìm được với nhau.
Ví dụ:
\(\begin{array}{l}({x^2}y + {y^2}x):xy\\ = {x^2}y:xy + {y^2}x:xy\\ = x + y\end{array}\)
Đa thức nhiều biến là một biểu thức đại số bao gồm các số, các biến và các phép toán cộng, trừ, nhân, chia giữa chúng. Việc nắm vững lý thuyết về đa thức nhiều biến là nền tảng quan trọng để giải quyết các bài toán đại số phức tạp hơn trong chương trình Toán 8 và các lớp học cao hơn.
Một đa thức nhiều biến là một biểu thức đại số có dạng:
P(x, y, z, ...) = anxnymzp... + an-1xn-1ym-1zp-1... + ... + a0
Trong đó:
Bậc của một đa thức nhiều biến là tổng số mũ của tất cả các biến trong một đơn thức của đa thức đó. Ví dụ:
Để cộng hoặc trừ hai đa thức, ta thực hiện cộng hoặc trừ các đơn thức đồng dạng. Đơn thức đồng dạng là các đơn thức có cùng phần biến và cùng bậc.
Ví dụ:
(2x2y + 3xy2) + (x2y - xy2) = (2x2y + x2y) + (3xy2 - xy2) = 3x2y + 2xy2
Để nhân hai đa thức, ta sử dụng tính chất phân phối của phép nhân đối với phép cộng. Tức là, ta nhân mỗi đơn thức của đa thức thứ nhất với mỗi đơn thức của đa thức thứ hai, sau đó cộng tất cả các kết quả lại.
Ví dụ:
(x + y)(x - y) = x(x - y) + y(x - y) = x2 - xy + xy - y2 = x2 - y2
Phép chia đa thức phức tạp hơn phép cộng, trừ, nhân. Để chia đa thức, ta thường sử dụng phương pháp chia đa thức một biến hoặc phương pháp đặt nhân tử chung.
Ví dụ (chia đa thức một biến):
(x2 + 2x + 1) : (x + 1) = x + 1
Để nắm vững lý thuyết và kỹ năng làm bài tập về đa thức nhiều biến, bạn nên luyện tập thường xuyên với các bài tập trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác. Hãy tìm kiếm các bài giảng trực tuyến, video hướng dẫn và các diễn đàn học tập để trao đổi kiến thức và kinh nghiệm với bạn bè và giáo viên.
Đa thức nhiều biến có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật, như:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết các phép tính với đa thức nhiều biến. Chúc bạn học tập tốt!