Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 69 SGK Toán 8 – Cánh diều. Bài học này thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:
Đề bài
Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:
a) Độ dài các đoạn thẳng BC, DB, DC;
b) Khoảng cách từ điểm D đến đường thẳng AC;
c) Độ dài đường phân giác AD
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định lý đường trung bình để tính độ dài các đoạn thẳng.
Lời giải chi tiết
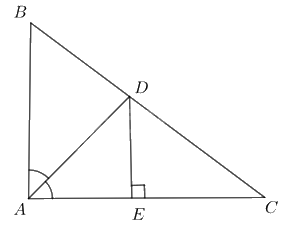
a) Tam giác ABC vuông tại A nên ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{3^2} + {4^2}} = 5\)
Vì AD là đường phân giác của tam giác ABC nên ta có:
\(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) (Tính chất đường phân giác trong tam giác)
Suy ra \(\frac{{DB}}{{DC}} = \frac{3}{4} \), do đó \(DB = \frac{3}{4}DC\)
Mà \(BD + CD = BC \)
Suy ra \(\frac{3}{4}CD + CD = 5 \)
\(CD = \frac{{20}}{7}\)
Do đó \(BD = 5 - \frac{{20}}{7} = \frac{{15}}{7}\).
b) Từ D kẻ đường thẳng vuông góc với AC cắt AC tại E. Khi đó DE là khoảng cách từ D đến đường thẳng AC.
Ta có: \(\left. \begin{array}{l}DE \bot AC\\AB \bot AC\end{array} \right\}\) suy ra \(DE// AB\)
Do đó \(\frac{{DE}}{{AB}} = \frac{{DC}}{{BC}} \)
\( \frac{{DE}}{3} = \frac{{\frac{{20}}{7}}}{5} \)
\(DE = \frac{{12}}{7}\) (Tính chất đường phân giác)
c) Xét tam giác ABC có \(DE// AB\) nên \(\frac{{BD}}{{BC}} = \frac{{AE}}{{AC}}\) (Định lý Thales)
Suy ra \( \frac{{\frac{{15}}{7}}}{5} = \frac{{AE}}{4} \) nên \(AE = \frac{{12}}{7}\)
Tam giác ADE vuông tại E nên ta có:
\(AD = \sqrt {A{E^2} + D{E^2}} = \sqrt {{{\left( {\frac{{12}}{7}} \right)}^2} + {{\left( {\frac{{12}}{7}} \right)}^2}} = \frac{{12\sqrt 2 }}{7}\)
Bài 5 trang 69 SGK Toán 8 – Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số để giải quyết các bài toán liên quan đến biểu thức đại số. Bài tập này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 5 trang 69 SGK Toán 8 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả bài 5 trang 69 SGK Toán 8 – Cánh diều, học sinh cần nắm vững các phương pháp sau:
Dưới đây là đáp án chi tiết cho từng bài tập trong bài 5 trang 69 SGK Toán 8 – Cánh diều:
(a + b) – (a – b) = a + b – a + b = 2b
Cho x = 2, y = -1. Tính giá trị của biểu thức 3x – 2y.
3x – 2y = 3(2) – 2(-1) = 6 + 2 = 8
Chứng minh rằng (x + y)^2 = x^2 + 2xy + y^2
(x + y)^2 = (x + y)(x + y) = x(x + y) + y(x + y) = x^2 + xy + yx + y^2 = x^2 + 2xy + y^2
Giải phương trình 2x + 3 = 7
2x = 7 – 3
2x = 4
x = 2
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 8 – Cánh diều hoặc trên các trang web học toán online.
Để học tốt môn Toán 8, học sinh cần:
Bài 5 trang 69 SGK Toán 8 – Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải bài tập đại số. Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong quá trình học tập.