Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 82 SGK Toán 8 – Cánh diều. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho
Đề bài
Cho \(\Delta ABC \backsim \Delta MNP\).
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh \(\Delta ABD \backsim \Delta MNQ\).
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh \(\Delta ABG \backsim \Delta MNK\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa tam giác đồng dạng để tìm điểm P.
Lời giải chi tiết
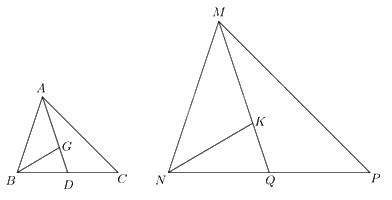
a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)
Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)
Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)
Xét tam giác ABD và tam giác MNQ có:
\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)
\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)
b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)
Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).
Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)
Xét tam giác ABG và tam giác NMK có:
\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)
\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)
Bài 5 trang 82 SGK Toán 8 – Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về các hình khối, đặc biệt là hình hộp chữ nhật và hình lập phương. Bài tập này không chỉ giúp củng cố lý thuyết mà còn rèn luyện kỹ năng giải toán không gian, một kỹ năng cần thiết cho các bài học nâng cao hơn.
Bài 5 trang 82 SGK Toán 8 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giải bài tập bài 5 trang 82 SGK Toán 8 – Cánh diều một cách hiệu quả, các em cần nắm vững các công thức sau:
Bài tập: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính thể tích và diện tích bề mặt của hình hộp chữ nhật đó.
Giải:
Thể tích của hình hộp chữ nhật là: V = 5 * 3 * 4 = 60 cm3.
Diện tích bề mặt của hình hộp chữ nhật là: S = 2 * (5 * 3 + 3 * 4 + 4 * 5) = 2 * (15 + 12 + 20) = 2 * 47 = 94 cm2.
Khi giải bài tập về hình hộp chữ nhật và hình lập phương, các em cần chú ý:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tự giải các bài tập sau:
Bài 5 trang 82 SGK Toán 8 – Cánh diều là một bài tập quan trọng giúp các em hiểu rõ hơn về hình hộp chữ nhật và hình lập phương. Bằng cách nắm vững các công thức và phương pháp giải bài tập, các em có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ học tập hiệu quả và đạt được thành công trong môn Toán.