Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 Cánh diều của giaitoan.edu.vn. Tại đây, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 8 Cánh diều, đặc biệt là các bài tập trang 66, 67 và 68.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong Hình 38, tam giác ABC có AD là đường phân giác của góc BAC.
Video hướng dẫn giải
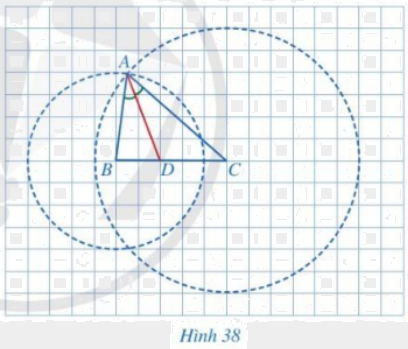
Trong Hình 38, tam giác ABC có AD là đường phân giác của góc BAC. Giả sử mỗi ô vuông của lưới ô vuông có độ dài cạnh bằng 1 cm.
a) Tính độ dài các đoạn thẳng DB, DC.
b) Tính độ dài các đoạn thẳng AB, AC.
c) So sánh các tỉ số \(\frac{{DB}}{{DC}},\,\,\frac{{AB}}{{AC}}\).
Phương pháp giải:
a) Đếm số ô tương ứng với các đoạn thẳng và tính độ dài.
b) AB và AC là bán kính của hai đường tròn.
c) Tính hai tỉ số và so sánh chúng.
Lời giải chi tiết:
a) Ta thấy mỗi ô vuông có độ dài cạnh bằng 1cm.
Đoạn thẳng BD có độ dài bằng độ dài cạnh của 2 ô vuông nên BD dài 2 cm.
Đoạn thẳng DC có độ dài bằng độ dài cạnh của 3 ô vuông nên BD dài 3 cm.
b) Ta thấy AB là bán kính đường tròn tâm B. Mà bán kính đường tròn tâm B có độ dài 4 ô vuông, tương ứng với 4 cm nên AB dài 4 cm.
Ta thấy AC là bán kính đường tròn tâm C. Mà bán kính đường tròn tâm C có độ dài 6 ô vuông, tương ứng với 6 cm nên AB dài 6 cm.
c) Ta có: \(\frac{{DB}}{{DC}} = \frac{2}{3};\,\,\frac{{AB}}{{AC}} = \frac{4}{6} = \frac{2}{3}\)
Vậy \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Video hướng dẫn giải
Cho tam giác ABC có \(AB < AC\), AD là đường phân giác. Chứng minh \(DB < DC\).
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.
Lời giải chi tiết:
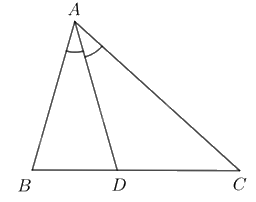
Xét tam giác ABC có AD là đường phân giác nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\)
Mà \(AB < AC\)\( \Rightarrow \frac{{AB}}{{AC}} < 1 \Rightarrow \frac{{DB}}{{DC}} < 1 \Rightarrow DB < DC\).
Video hướng dẫn giải
Giải bài toán nêu trong phần mở đầu.
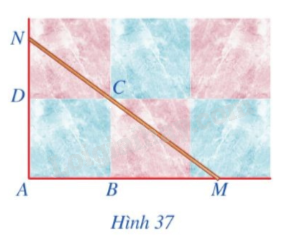
Bài toán: Hình 37 minh họa một phần sân nhà bạn Duy được lát bởi các viên gạch hình vuông khít nhau, trong đó các điểm A, B, C, D là bốn đỉnh của một viên gạch. Bạn Duy đặt một thước gỗ trên mặt sân sao cho thước gỗ luôn đi qua điểm C và cắt tia AB tại M, cắt tia AD tại N. Bạn Duy nhận thấy ta luôn có tỉ lệ thức \(\frac{CM}{CN} = \frac{AM}{AN}\)
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh.
Lời giải chi tiết:
Ta có ABCD là hình vuông có AC là đường chéo nên góc DAC bằng góc CAB.
Hay góc NAC bằng góc MAC.
Suy ra: AC là đường phân giác của góc MAN.
Theo định lí đường phân giác của tam giác ta có:
\(\frac{CM}{CN} = \frac{AM}{AN}\)
Video hướng dẫn giải
Cho tam giác ABC, điểm D thuộc cạnh BC sao cho \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\). Chứng minh AD là tia phân giác của góc BAC.
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.
Lời giải chi tiết:
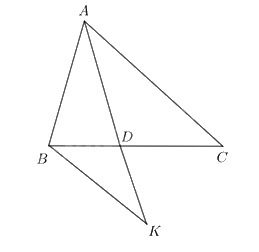
Từ B kẻ đường thẳng song song với AC, cắt AD tại K.
Vì \(BK//AC\) nên theo hệ quả của định lý Thales, ta có: \(\frac{{DB}}{{DC}} = \frac{{BK}}{{AC}}\)
Mà \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) nên \(\frac{{BK}}{{AC}} = \frac{{AB}}{{AC}} \Rightarrow AB = BK\)
Khi đó tam giác ABK cân tại B nên \(\widehat {BAK} = \widehat {BKA}\)
Mà \(BK//AC\) nên \(\widehat {BKA} = \widehat {KAC}\)
\( \Rightarrow \widehat {BAK} = \widehat {KAC}\)
Vậy AD là đường phân giác trong tam giác ABC.
Video hướng dẫn giải
Cho tam giác ABC có ba đường phân giác AD, BE, CF. Chứng minh \(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 1\)
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.
Lời giải chi tiết:
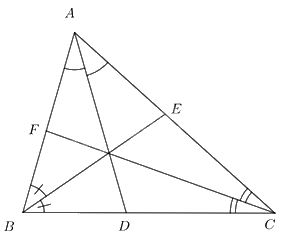
Xét tam giác ABC với ba đường phân giác AD, BE, CF, ta có:
\(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}};\,\,\frac{{BC}}{{BA}} = \frac{{EC}}{{EA}};\,\,\frac{{CA}}{{CB}} = \frac{{FA}}{{FB}}\) (Tính chất đường phân giác)
\( \Rightarrow \frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{{AB}}{{AC}}.\frac{{BC}}{{BA}}.\frac{{CA}}{{CB}} = \frac{{AB.BC.CA}}{{CA.AB.BC}} = 1\) (đpcm).
Video hướng dẫn giải
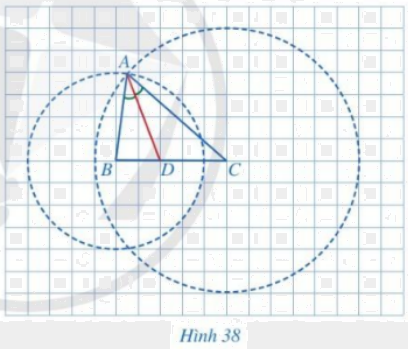
Trong Hình 38, tam giác ABC có AD là đường phân giác của góc BAC. Giả sử mỗi ô vuông của lưới ô vuông có độ dài cạnh bằng 1 cm.
a) Tính độ dài các đoạn thẳng DB, DC.
b) Tính độ dài các đoạn thẳng AB, AC.
c) So sánh các tỉ số \(\frac{{DB}}{{DC}},\,\,\frac{{AB}}{{AC}}\).
Phương pháp giải:
a) Đếm số ô tương ứng với các đoạn thẳng và tính độ dài.
b) AB và AC là bán kính của hai đường tròn.
c) Tính hai tỉ số và so sánh chúng.
Lời giải chi tiết:
a) Ta thấy mỗi ô vuông có độ dài cạnh bằng 1cm.
Đoạn thẳng BD có độ dài bằng độ dài cạnh của 2 ô vuông nên BD dài 2 cm.
Đoạn thẳng DC có độ dài bằng độ dài cạnh của 3 ô vuông nên BD dài 3 cm.
b) Ta thấy AB là bán kính đường tròn tâm B. Mà bán kính đường tròn tâm B có độ dài 4 ô vuông, tương ứng với 4 cm nên AB dài 4 cm.
Ta thấy AC là bán kính đường tròn tâm C. Mà bán kính đường tròn tâm C có độ dài 6 ô vuông, tương ứng với 6 cm nên AB dài 6 cm.
c) Ta có: \(\frac{{DB}}{{DC}} = \frac{2}{3};\,\,\frac{{AB}}{{AC}} = \frac{4}{6} = \frac{2}{3}\)
Vậy \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Video hướng dẫn giải
Giải bài toán nêu trong phần mở đầu.
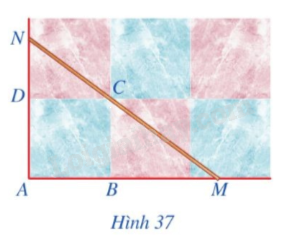
Bài toán: Hình 37 minh họa một phần sân nhà bạn Duy được lát bởi các viên gạch hình vuông khít nhau, trong đó các điểm A, B, C, D là bốn đỉnh của một viên gạch. Bạn Duy đặt một thước gỗ trên mặt sân sao cho thước gỗ luôn đi qua điểm C và cắt tia AB tại M, cắt tia AD tại N. Bạn Duy nhận thấy ta luôn có tỉ lệ thức \(\frac{CM}{CN} = \frac{AM}{AN}\)
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh.
Lời giải chi tiết:
Ta có ABCD là hình vuông có AC là đường chéo nên góc DAC bằng góc CAB.
Hay góc NAC bằng góc MAC.
Suy ra: AC là đường phân giác của góc MAN.
Theo định lí đường phân giác của tam giác ta có:
\(\frac{CM}{CN} = \frac{AM}{AN}\)
Video hướng dẫn giải
Cho tam giác ABC có \(AB < AC\), AD là đường phân giác. Chứng minh \(DB < DC\).
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.
Lời giải chi tiết:
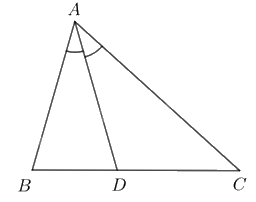
Xét tam giác ABC có AD là đường phân giác nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\)
Mà \(AB < AC\)\( \Rightarrow \frac{{AB}}{{AC}} < 1 \Rightarrow \frac{{DB}}{{DC}} < 1 \Rightarrow DB < DC\).
Video hướng dẫn giải
Cho tam giác ABC có ba đường phân giác AD, BE, CF. Chứng minh \(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 1\)
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.
Lời giải chi tiết:
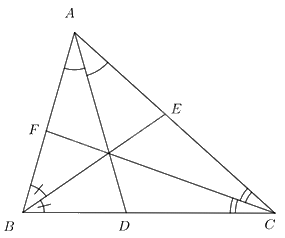
Xét tam giác ABC với ba đường phân giác AD, BE, CF, ta có:
\(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}};\,\,\frac{{BC}}{{BA}} = \frac{{EC}}{{EA}};\,\,\frac{{CA}}{{CB}} = \frac{{FA}}{{FB}}\) (Tính chất đường phân giác)
\( \Rightarrow \frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{{AB}}{{AC}}.\frac{{BC}}{{BA}}.\frac{{CA}}{{CB}} = \frac{{AB.BC.CA}}{{CA.AB.BC}} = 1\) (đpcm).
Video hướng dẫn giải
Cho tam giác ABC, điểm D thuộc cạnh BC sao cho \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\). Chứng minh AD là tia phân giác của góc BAC.
Phương pháp giải:
Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.
Lời giải chi tiết:
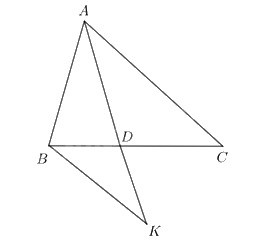
Từ B kẻ đường thẳng song song với AC, cắt AD tại K.
Vì \(BK//AC\) nên theo hệ quả của định lý Thales, ta có: \(\frac{{DB}}{{DC}} = \frac{{BK}}{{AC}}\)
Mà \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) nên \(\frac{{BK}}{{AC}} = \frac{{AB}}{{AC}} \Rightarrow AB = BK\)
Khi đó tam giác ABK cân tại B nên \(\widehat {BAK} = \widehat {BKA}\)
Mà \(BK//AC\) nên \(\widehat {BKA} = \widehat {KAC}\)
\( \Rightarrow \widehat {BAK} = \widehat {KAC}\)
Vậy AD là đường phân giác trong tam giác ABC.
Chương trình Toán 8 Cánh diều tập trung vào việc xây dựng nền tảng vững chắc cho các em học sinh trước khi bước vào các chương trình Toán nâng cao hơn. Trang 66, 67 và 68 của SGK Toán 8 Cánh diều thường chứa các bài tập liên quan đến các chủ đề quan trọng như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, và hệ phương trình bậc nhất hai ẩn. Việc nắm vững các kiến thức này là vô cùng quan trọng để giải quyết các bài toán phức tạp hơn trong tương lai.
Các bài tập trên trang 66 thường tập trung vào việc vận dụng các kiến thức về đa thức để thực hiện các phép toán cộng, trừ, nhân, chia đa thức. Các em cần nắm vững các quy tắc về dấu, bậc của đa thức, và các phương pháp phân tích đa thức thành nhân tử để giải quyết các bài tập này một cách hiệu quả.
Trang 67 thường chứa các bài tập liên quan đến phân thức đại số. Các em cần hiểu rõ khái niệm phân thức, các quy tắc rút gọn phân thức, quy đồng mẫu số, và thực hiện các phép toán cộng, trừ, nhân, chia phân thức. Ngoài ra, các em cũng cần lưu ý đến điều kiện xác định của phân thức để tránh các lỗi sai không đáng có.
Các bài tập trên trang 68 thường liên quan đến phương trình bậc nhất một ẩn. Các em cần nắm vững các bước giải phương trình, các quy tắc biến đổi tương đương, và các ứng dụng của phương trình bậc nhất một ẩn trong việc giải quyết các bài toán thực tế.
Bài tập: Giải phương trình 2x + 3 = 7
Lời giải:
Khi giải bài tập Toán 8 Cánh diều, các em cần chú ý đến các điều kiện xác định của các biểu thức, các quy tắc về dấu, bậc của đa thức, và các phương pháp phân tích đa thức thành nhân tử. Ngoài ra, các em cũng cần rèn luyện kỹ năng giải toán thường xuyên để nâng cao khả năng giải quyết các bài toán phức tạp.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trang 66, 67, 68 SGK Toán 8 Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!