Chào mừng bạn đến với bài học lý thuyết Tứ giác trong chương trình Toán 8, sách Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về tứ giác, giúp bạn hiểu rõ các khái niệm, tính chất và ứng dụng của nó trong giải toán.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và bài tập thực hành đa dạng để bạn có thể tự tin chinh phục môn Toán.
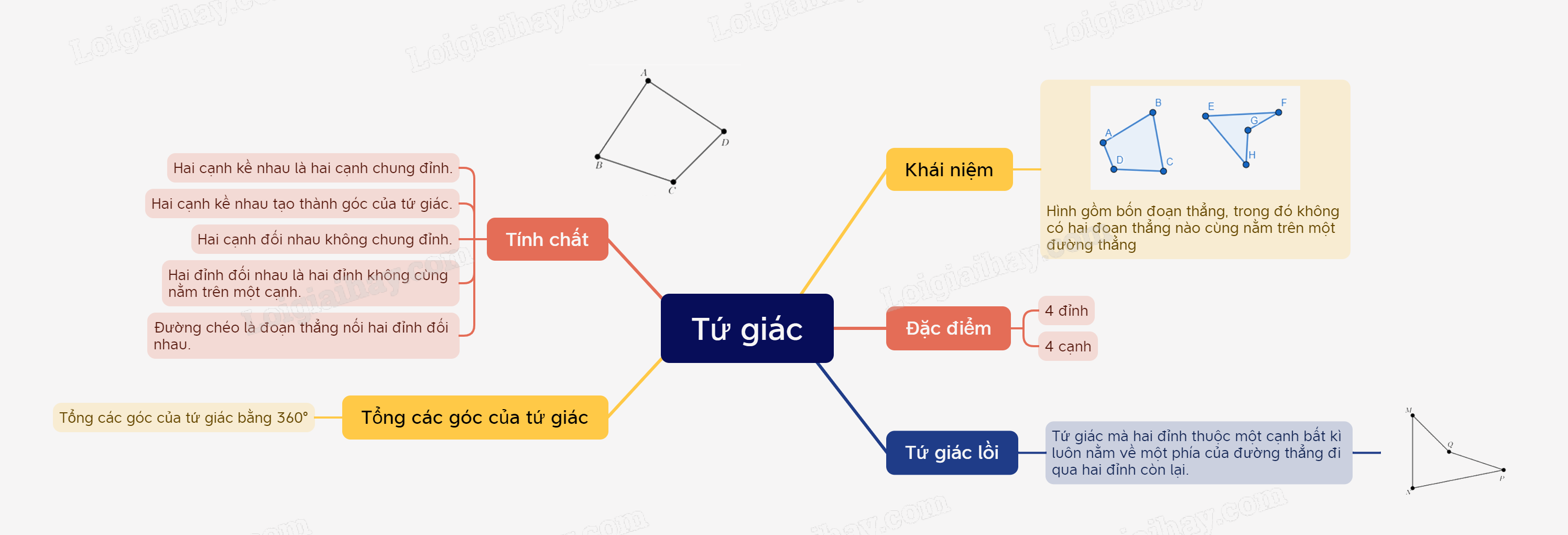
Tứ giác là gì?
1. Khái niệm
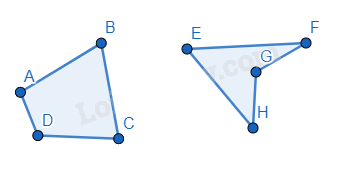
Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Ví dụ:
Đặc điểm
+Có 4 đỉnh
+ Có 4 cạnh
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa bất kỳ cạnh nào của tứ giác đó.
Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.
2. Tính chất:
+Hai cạnh kề nhau là hai cạnh chung đỉnh.
+ Hai cạnh kề nhau tạo thành góc của tứ giác.
+ Hai cạnh đối nhau không chung đỉnh.
+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.
+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
3. Định lí tổng các góc của một tứ giác
Tổng số đo các góc của một tứ giác bằng \({360^0}\).
Tứ giác ABCD, \(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\)
Ví dụ:
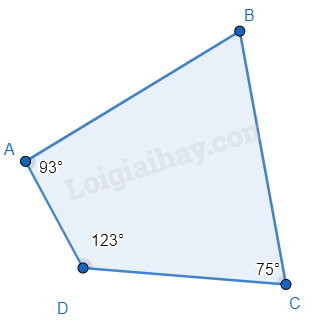
\(\widehat B = {360^0} - {93^0} - {123^0} - {75^0} = {69^0}\)
Tứ giác là một trong những khái niệm cơ bản và quan trọng trong hình học lớp 8. Hiểu rõ về tứ giác là nền tảng để giải quyết nhiều bài toán phức tạp hơn trong chương trình học. Bài viết này sẽ trình bày chi tiết lý thuyết về tứ giác theo sách giáo khoa Toán 8 - Cánh diều, bao gồm định nghĩa, các loại tứ giác đặc biệt, tính chất và ứng dụng.
Tứ giác là hình có bốn cạnh và bốn góc. Bốn đỉnh của tứ giác là bốn điểm không cùng nằm trên một đường thẳng. Ký hiệu tứ giác ABCD được viết là tứ giác ABCD, với A, B, C, D là các đỉnh của tứ giác.
Có nhiều loại tứ giác đặc biệt, mỗi loại có những tính chất riêng:
Tổng bốn góc của một tứ giác bằng 360 độ. Đây là tính chất cơ bản và quan trọng nhất của tứ giác, được sử dụng để giải nhiều bài toán liên quan đến tứ giác.
Mỗi loại tứ giác đặc biệt có những tính chất riêng:
Lý thuyết tứ giác được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là trong việc chứng minh các tính chất của hình, tính độ dài các đoạn thẳng, tính số đo các góc và giải các bài toán thực tế.
Để củng cố kiến thức về tứ giác, bạn có thể thực hành giải các bài tập sau:
Lý thuyết tứ giác là một phần quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập sẽ giúp bạn tự tin hơn trong việc học tập và giải quyết các vấn đề liên quan đến hình học. Hãy luyện tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn.
| Loại Tứ giác | Tính chất |
|---|---|
| Hình thang | Hai cạnh đối song song |
| Hình bình hành | Hai cặp cạnh đối song song và bằng nhau |
| Hình chữ nhật | Bốn góc vuông |