Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 81 SGK Toán 8 – Cánh diều tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài giải này được xây dựng bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và phù hợp với chương trình học.
Cho hai tam giác ABC và A’B’C’ có
Video hướng dẫn giải
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\). Chứng minh \(\widehat B = \widehat {B'}\).
Phương pháp giải:
- Từ tỉ lệ đã cho, suy ra tỉ lệ để chứng minh hai tam giác ABC và A’B’C’ đồng dạng theo trường hợp đồng dạng thứ hai.
- Suy ra hai góc bằng nhau theo định nghĩa tam giác đồng dạng.
Lời giải chi tiết:
Ta có: \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\)
Hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ nên \(\widehat {A'} = \widehat A = 90^\circ \).
Xét tam giác ABC và tam giác A’B’C’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) và \(\widehat {A'} = \widehat A\)
\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\) (c-g-c)
\( \Rightarrow \widehat B = \widehat {B'}\).
Video hướng dẫn giải
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) (Hình 72). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\)
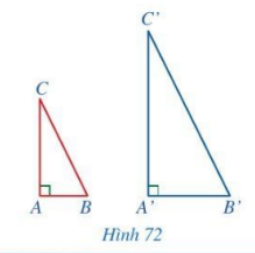
Phương pháp giải:
Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác đồng dạng.
Lời giải chi tiết:
Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)
Video hướng dẫn giải
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\). Chứng minh \(\widehat B = \widehat {B'}\).
Phương pháp giải:
- Từ tỉ lệ đã cho, suy ra tỉ lệ để chứng minh hai tam giác ABC và A’B’C’ đồng dạng theo trường hợp đồng dạng thứ hai.
- Suy ra hai góc bằng nhau theo định nghĩa tam giác đồng dạng.
Lời giải chi tiết:
Ta có: \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\)
Hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ nên \(\widehat {A'} = \widehat A = 90^\circ \).
Xét tam giác ABC và tam giác A’B’C’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) và \(\widehat {A'} = \widehat A\)
\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\) (c-g-c)
\( \Rightarrow \widehat B = \widehat {B'}\).
Video hướng dẫn giải
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) (Hình 72). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\)
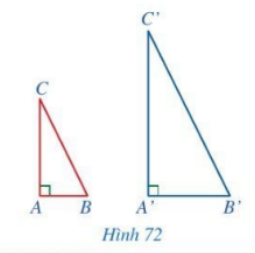
Phương pháp giải:
Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác đồng dạng.
Lời giải chi tiết:
Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)
Mục 2 trang 81 SGK Toán 8 – Cánh diều tập trung vào việc vận dụng các kiến thức đã học về hình hộp chữ nhật và hình lập phương để giải các bài toán thực tế. Các bài tập thường yêu cầu tính thể tích, diện tích bề mặt, hoặc xác định các yếu tố của hình.
Lời giải:
Thể tích của hình hộp chữ nhật là: V = 5cm * 4cm * 3cm = 60cm3
Lời giải:
Diện tích bề mặt của hình lập phương là: S = 6 * (2cm)2 = 24cm2
Lời giải:
Thể tích của bể nước là: V = 1.2m * 0.8m * 1m = 0.96m3
Lời giải:
Diện tích các bức tường bên trong phòng học là: 2 * (8m * 4m) + 2 * (6m * 4m) = 64m2 + 48m2 = 112m2
Diện tích cần quét vôi là: 112m2 - 10m2 = 102m2
Kiến thức về hình hộp chữ nhật và hình lập phương có ứng dụng rộng rãi trong thực tế, như:
Để củng cố kiến thức và kỹ năng giải bài tập về hình hộp chữ nhật và hình lập phương, các em có thể luyện tập thêm các bài tập trong SGK Toán 8 – Cánh diều và các tài liệu tham khảo khác. Giaitoan.edu.vn sẽ tiếp tục cập nhật thêm nhiều bài giải và tài liệu học tập hữu ích cho các em.