Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 3 trang 97, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán. Hãy cùng bắt đầu với bài 3 trang 97 nhé!
Cho tam giác vuông cân
Đề bài
Cho tam giác vuông cân có độ dài cạnh góc vuông bằng 1 dm. Tính độ dài cạnh huyền của tam giác đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pythagore trong tam giác vuông cân đó.
Lời giải chi tiết
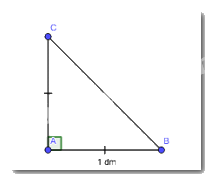
Giả sử \(\Delta ABC\) vuông cân tại A có AB =AC = 1dm.
Áp dụng định lí Pythagone trong \(\Delta ABC\) vuông cân tại A.
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} = {1^2} + {1^2} = 2\\ \Rightarrow BC = \sqrt 2 dm\end{array}\)
Độ dài cạnh huyền bằng \(\sqrt 2 dm\)
Bài 3 trang 97 SGK Toán 8 tập 1 - Cánh diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông để giải quyết các bài toán thực tế.
Bài 3 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài 3 trang 97 SGK Toán 8 tập 1 - Cánh diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Giả sử chúng ta có một hình chữ nhật ABCD, với AB = 5cm và BC = 3cm. Hãy tính độ dài đường chéo AC.
Giải:
Vì ABCD là hình chữ nhật, nên góc ABC là góc vuông. Do đó, tam giác ABC là tam giác vuông tại B. Áp dụng định lý Pitago, ta có:
AC2 = AB2 + BC2
AC2 = 52 + 32 = 25 + 9 = 34
AC = √34 ≈ 5.83cm
Bài 3 trang 97 SGK Toán 8 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về các hình bình hành, hình chữ nhật, hình thoi và hình vuông. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!