Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 64 SGK Toán 8 tập 1 - Cánh diều. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Điểm M (a; b) thuộc góc phần tư nào trong mỗi trường hợp sau:
Đề bài
Điểm M (a; b) thuộc góc phần tư nào trong mỗi trường hợp sau:
a) a>0; b>0
b) a>0; b<0
c) a<0; b>0
d) a<0; b<0
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Quan sát các góc phần tư có trong hình sau về giá trị của tung độ, giá trị của hoành độ.
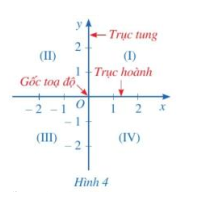
Lời giải chi tiết
a) a>0; b>0 thì M(a; b) thuộc góc phần tư thứ nhất.
b) a>0; b
c) a<0; b>0 thì M(a; b) thuộc góc phần tư thứ hai.
d) a<0; b
Bài 2 trang 64 SGK Toán 8 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số để rút gọn biểu thức và tìm giá trị của biểu thức. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các phép toán cộng, trừ, nhân, chia đa thức.
Bài 2 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các phép toán khác nhau. Chúng ta sẽ cùng nhau phân tích từng câu hỏi và tìm ra lời giải chính xác nhất.
Để rút gọn biểu thức này, chúng ta sử dụng công thức phân phối (a + b)(c + d) = ac + ad + bc + bd.
(2x + 3)(x - 1) = 2x * x + 2x * (-1) + 3 * x + 3 * (-1) = 2x2 - 2x + 3x - 3 = 2x2 + x - 3
Để tìm giá trị của biểu thức, chúng ta thay x = 2 vào biểu thức và thực hiện các phép tính.
3 * (2)2 - 5 * (2) + 2 = 3 * 4 - 10 + 2 = 12 - 10 + 2 = 4
Để chứng minh điều này, chúng ta khai triển hai bình phương và thực hiện các phép toán.
(x + 2)2 - (x - 2)2 = (x2 + 4x + 4) - (x2 - 4x + 4) = x2 + 4x + 4 - x2 + 4x - 4 = 8x
Tuy nhiên, kết quả là 8x chứ không phải 8. Có lẽ đề bài có sai sót. Nếu đề bài là chứng minh (x+2)(x-2) = x2 - 4 thì:
(x+2)(x-2) = x2 - 2x + 2x - 4 = x2 - 4
Để giải các bài tập tương tự, các em cần:
Hãy cùng xét ví dụ sau: Rút gọn biểu thức (x + 1)(x - 2) + x2.
(x + 1)(x - 2) + x2 = x2 - 2x + x - 2 + x2 = 2x2 - x - 2
Khi giải bài tập về biểu thức đại số, các em cần chú ý đến thứ tự thực hiện các phép toán. Luôn thực hiện các phép toán trong ngoặc trước, sau đó đến các phép nhân, chia, và cuối cùng là các phép cộng, trừ.
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học Toán 8. Chúc các em học tập tốt!