Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 - Cánh diều. Mục 2 trang 106 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các định lý và tính chất đã học.
Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin giải các bài tập tương tự.
Cho hình bình hành ABCD (Hình 37). a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC. b) So sánh các cặp góc:
Video hướng dẫn giải
Cho hình bình hành ABCD có \(\widehat A = {80^o};AB = 4cm;BC = 5cm\). Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.
Phương pháp giải:
Vận dụng tính chất của hình bình hành.
Lời giải chi tiết:
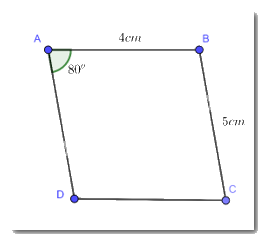
Do ABCD là hình bình hành
Suy ra: CD = AB = 4cm
AD = BC = 5 cm
\(\widehat C = \widehat A = {80^o}\)
Nên: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{80}^o} - {{80}^o}}}{2} = {100^o}\)
Video hướng dẫn giải
Cho hình bình hành ABCD (Hình 37).
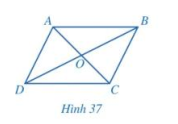
a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC.
b) So sánh các cặp góc: \(\widehat {DAB}\) và \(\widehat {BCD}\); \(\widehat {ABC}\) và \(\widehat {CDA}\).
c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.
Phương pháp giải:
Sử dụng chứng minh các tam giác tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét tam giác ABD và tam giác CDB có:
\(\widehat {ABD} = \widehat {CDB}\) ( vì AB //CD)
BD chung
\(\widehat {ADB} = \widehat {CBD}\) (vì AD // BC)
Suy ra: \(\Delta ABD = \Delta CDB\)(g - c - g)
Suy ra: AB = CD, DA = BC.
b) Vì \(\Delta AB{\rm{D}} = \Delta C{\rm{D}}B\) (g - c - g) suy ra: \(\widehat {DAB}\) = \(\widehat {BCD}\)
Xét tam giác ABC và tam giác CDA có:
AB = CD (cmt)
Cạnh AC chung
BC = AD (cmt)
\(\Delta ABC = \Delta CDA (c - c - c) \Rightarrow \widehat {ABC} = \widehat {CDA}\) (2 góc tương ứng)
c) Xét tam giác OAB và OCD có:
\(\begin{array}{l}\widehat {OAB} = \widehat {OCD} (cmt)\\AB = CD (cmt)\\\widehat {OBA} = \widehat {ODC} (cmt)\end{array}\)
Suy ra: \(\Delta OAB = \Delta OC{\rm{D}}\) (g - c - g) suy ra: OA = OC; OB = OD (các cạnh tương ứng)
Video hướng dẫn giải
Cho hình bình hành ABCD (Hình 37).
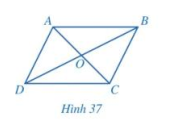
a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC.
b) So sánh các cặp góc: \(\widehat {DAB}\) và \(\widehat {BCD}\); \(\widehat {ABC}\) và \(\widehat {CDA}\).
c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.
Phương pháp giải:
Sử dụng chứng minh các tam giác tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét tam giác ABD và tam giác CDB có:
\(\widehat {ABD} = \widehat {CDB}\) ( vì AB //CD)
BD chung
\(\widehat {ADB} = \widehat {CBD}\) (vì AD // BC)
Suy ra: \(\Delta ABD = \Delta CDB\)(g - c - g)
Suy ra: AB = CD, DA = BC.
b) Vì \(\Delta AB{\rm{D}} = \Delta C{\rm{D}}B\) (g - c - g) suy ra: \(\widehat {DAB}\) = \(\widehat {BCD}\)
Xét tam giác ABC và tam giác CDA có:
AB = CD (cmt)
Cạnh AC chung
BC = AD (cmt)
\(\Delta ABC = \Delta CDA (c - c - c) \Rightarrow \widehat {ABC} = \widehat {CDA}\) (2 góc tương ứng)
c) Xét tam giác OAB và OCD có:
\(\begin{array}{l}\widehat {OAB} = \widehat {OCD} (cmt)\\AB = CD (cmt)\\\widehat {OBA} = \widehat {ODC} (cmt)\end{array}\)
Suy ra: \(\Delta OAB = \Delta OC{\rm{D}}\) (g - c - g) suy ra: OA = OC; OB = OD (các cạnh tương ứng)
Video hướng dẫn giải
Cho hình bình hành ABCD có \(\widehat A = {80^o};AB = 4cm;BC = 5cm\). Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.
Phương pháp giải:
Vận dụng tính chất của hình bình hành.
Lời giải chi tiết:
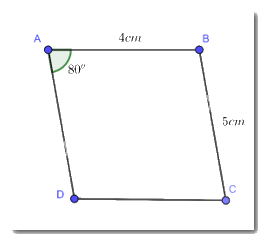
Do ABCD là hình bình hành
Suy ra: CD = AB = 4cm
AD = BC = 5 cm
\(\widehat C = \widehat A = {80^o}\)
Nên: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{80}^o} - {{80}^o}}}{2} = {100^o}\)
Mục 2 trang 106 SGK Toán 8 tập 1 - Cánh diều thường tập trung vào việc vận dụng các kiến thức đã học trong chương để giải quyết các bài toán thực tế. Các bài toán này có thể liên quan đến việc chứng minh các đẳng thức, giải phương trình, hoặc áp dụng các định lý để tính toán các yếu tố hình học.
Mục 2 thường bao gồm các bài tập sau:
Để giải tốt các bài tập trong Mục 2 trang 106, bạn cần nắm vững các kiến thức sau:
Dưới đây là giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 106 SGK Toán 8 tập 1 - Cánh diều:
Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh AD là đường phân giác của góc BAC.
Giải:
Vì tam giác ABC cân tại A và D là trung điểm của BC nên AD là đường trung tuyến đồng thời là đường cao của tam giác ABC. Do đó, AD vuông góc với BC. Xét hai tam giác ABD và ACD, ta có:
Vậy, tam giác ABD = tam giác ACD (c-c-c). Suy ra, góc BAD = góc CAD. Do đó, AD là đường phân giác của góc BAC.
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chứng minh AM = BM = CM.
Giải:
Vì tam giác ABC vuông tại A và M là trung điểm của BC nên AM là đường trung tuyến ứng với cạnh huyền BC. Theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có AM = BM = CM.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn nên làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn học khác.
Toán 8 là một môn học quan trọng, đòi hỏi sự chăm chỉ và kiên trì. Để học tốt Toán 8, bạn nên:
Chúc bạn học tốt Toán 8!