Định lí Pythagore là một trong những định lý quan trọng nhất trong hình học, được học trong chương trình Toán 8. Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu về lý thuyết Định lí Pythagore trong sách giáo khoa Toán 8 - Cánh diều.
Chúng ta sẽ cùng nhau tìm hiểu về nội dung định lý, cách chứng minh, các ứng dụng thực tế và các bài tập minh họa để giúp bạn nắm vững kiến thức này.
Định lí Pythagore
1. Định lí Pythagore
Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
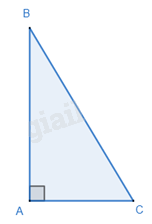
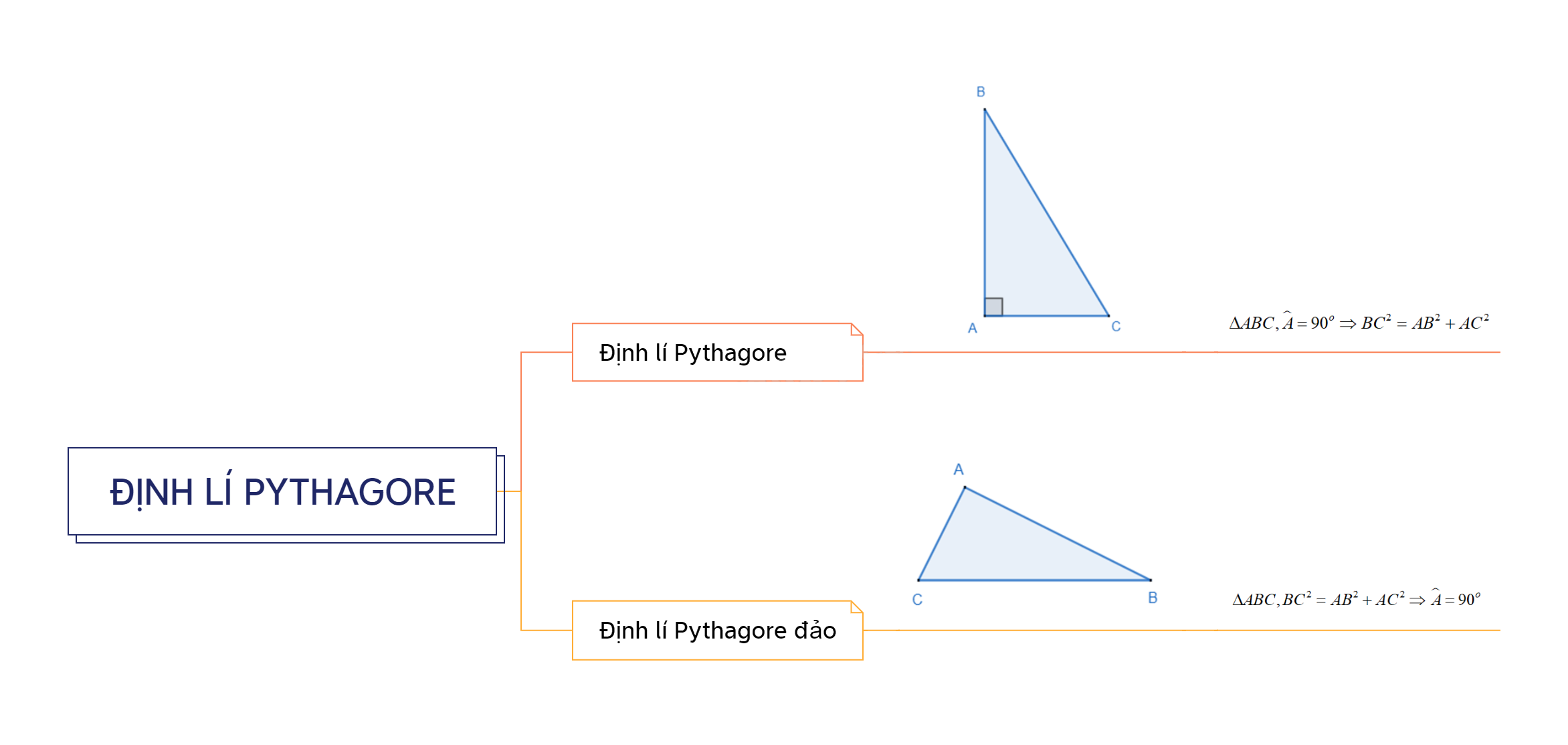
\(\Delta ABC,\widehat A = {90^o} \) suy ra \(B{C^2} = A{B^2} + A{C^2}\)
2. Định lí Pythagore đảo
Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.
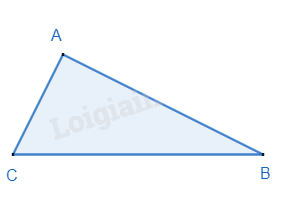
\(\Delta ABC,B{C^2} = A{B^2} + A{C^2} \) suy ra \( \widehat A = {90^o}\)
Ví dụ:
Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do \({3^2} + {4^2} = {5^2}\), suy ra \(B{C^2} = A{B^2} + A{C^2}\).
Định lí Pythagore là nền tảng của hình học tam giác vuông, và việc hiểu rõ lý thuyết này là rất quan trọng để giải quyết các bài toán liên quan. Bài viết này sẽ trình bày chi tiết lý thuyết Định lí Pythagore theo chương trình SGK Toán 8 - Cánh diều, giúp học sinh nắm vững kiến thức và áp dụng vào thực tế.
Trước khi đi vào Định lí Pythagore, chúng ta cần hiểu rõ về tam giác vuông. Tam giác vuông là tam giác có một góc vuông (90 độ). Trong một tam giác vuông:
Định lí Pythagore phát biểu rằng: Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.
Công thức toán học của Định lí Pythagore là:
a2 + b2 = c2
Trong đó:
Có nhiều cách chứng minh Định lí Pythagore, dưới đây là một trong những cách chứng minh phổ biến nhất:
(Phần này sẽ trình bày chi tiết một cách chứng minh Định lí Pythagore bằng hình vẽ và giải thích cụ thể. Có thể sử dụng hình ảnh minh họa để tăng tính trực quan.)
Định lí Pythagore có rất nhiều ứng dụng trong thực tế, bao gồm:
Dưới đây là một số bài tập vận dụng Định lí Pythagore:
(Phần này sẽ cung cấp lời giải chi tiết cho từng bài tập, giúp học sinh hiểu rõ cách áp dụng Định lí Pythagore vào giải quyết các bài toán cụ thể.)
Ngoài các bài tập cơ bản, Định lí Pythagore còn xuất hiện trong nhiều dạng bài tập khác nhau. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về Lý thuyết Định lí Pythagore SGK Toán 8 - Cánh diều. Chúc bạn học tập tốt!