Bài viết này cung cấp đầy đủ và chi tiết lý thuyết về Trường hợp đồng dạng thứ nhất của tam giác, thuộc chương trình Toán 8, sách Cánh diều. Chúng tôi sẽ giúp bạn hiểu rõ các khái niệm, định lý và cách áp dụng vào giải bài tập một cách hiệu quả.
Với phương pháp trình bày dễ hiểu, kèm theo ví dụ minh họa, bạn sẽ dễ dàng nắm bắt kiến thức và tự tin giải quyết các bài toán liên quan đến đồng dạng tam giác.
Trường hợp đồng dạng thứ nhất của tam giác là gì?
1. Trường hợp đồng dạng thứ nhất: Cạnh – cạnh – cạnh
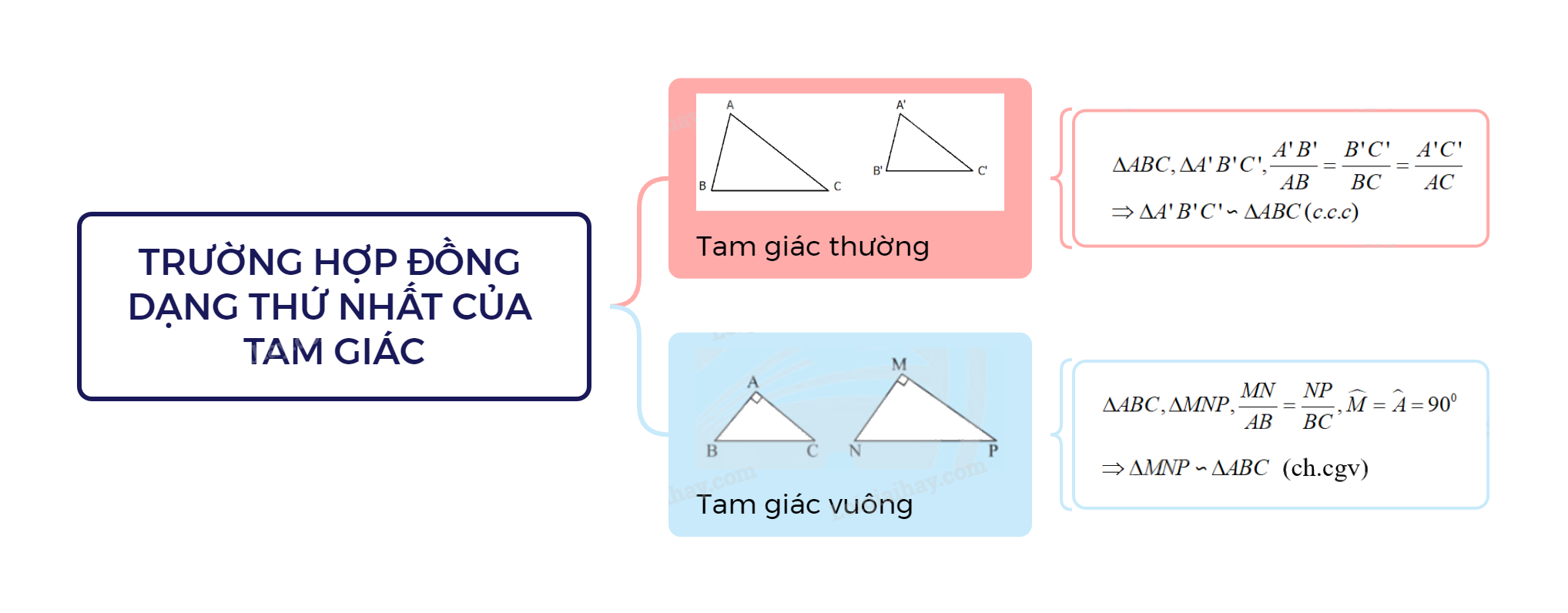
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
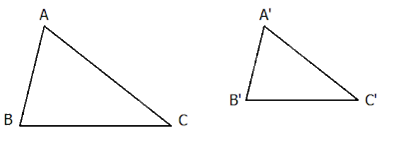
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,(c.c.c)\end{array}\)
2. Trường hợp đồng dạng thứ nhất của tam giác vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
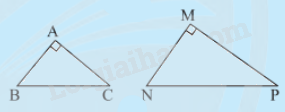
\(\Delta ABC,\Delta MNP,\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}},\widehat M = \widehat A = {90^0}\)
\( \Rightarrow \Delta MNP \backsim \Delta ABC\,\) (ch.cgv)
Trong chương trình Toán 8, phần học về tam giác đồng dạng đóng vai trò quan trọng, giúp học sinh hiểu rõ hơn về mối quan hệ giữa các tam giác và ứng dụng trong giải toán. Một trong những kiến thức cơ bản nhất là Trường hợp đồng dạng thứ nhất của tam giác. Bài viết này sẽ đi sâu vào lý thuyết này, cung cấp kiến thức chi tiết và dễ hiểu, giúp các em học sinh nắm vững kiến thức và áp dụng vào giải bài tập một cách hiệu quả.
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Kí hiệu: ΔABC ~ ΔA'B'C' (đọc là tam giác ABC đồng dạng với tam giác A'B'C').
Điều kiện để ΔABC ~ ΔA'B'C':
Định lý: Nếu hai tam giác có một góc bằng nhau và hai cạnh kề góc đó tỉ lệ thì hai tam giác đó đồng dạng.
Tóm tắt:
ΔABC ~ ΔA'B'C' nếu:
Chứng minh định lý này dựa trên việc xây dựng tam giác đồng dạng bằng cách sử dụng các đoạn thẳng tương ứng tỉ lệ và góc bằng nhau. Việc chứng minh này thường được thực hiện trong sách giáo khoa và các tài liệu tham khảo.
Ví dụ 1: Cho ΔABC có ∠A = 60°, AB = 4cm, AC = 6cm. Cho ΔA'B'C' có ∠A' = 60°, A'B' = 2cm, A'C' = 3cm. Chứng minh ΔABC ~ ΔA'B'C'.
Giải:
Xét ΔABC và ΔA'B'C' có:
Do đó, AB/A'B' = AC/A'C' = 2. Vậy, ΔABC ~ ΔA'B'C' (theo trường hợp đồng dạng thứ nhất).
Ví dụ 2: (Bài tập SGK Toán 8 - Cánh diều)
(Nội dung bài tập và lời giải được trình bày chi tiết)
Trường hợp đồng dạng thứ nhất được sử dụng rộng rãi trong việc:
Để củng cố kiến thức về Trường hợp đồng dạng thứ nhất, các em học sinh nên thực hành giải nhiều bài tập khác nhau. Dưới đây là một số bài tập gợi ý:
Hy vọng bài viết này đã cung cấp cho các em học sinh những kiến thức cần thiết về Lý thuyết Trường hợp đồng dạng thứ nhất của tam giác SGK Toán 8 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!