Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 110, 111 SGK Toán 8 tập 1 - Cánh diều trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em học sinh chinh phục môn Toán một cách dễ dàng.
a) Cho hình bình hành ABCD có (widehat A = {90^o}). ABCD có phải là hình chữ nhật hay không? b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50) Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh (widehat {ABC}) và (widehat {DCB}). ABCD có phải là hình chữ nhật hay không?
Video hướng dẫn giải
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn \(\widehat {OAB} = \widehat {O{\rm{D}}C}\). Chứng minh ABCD là hình chữ nhật.
Phương pháp giải:
Chứng minh hình bình hành ABCD có AC = BD.
Lời giải chi tiết:
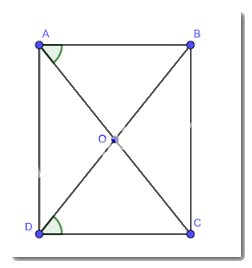
Do ABCD là hình bình hành suy ra AB = CD và AB // CD nên \(\widehat{ABO}=\widehat{ODC}\) (hai góc so le trong\)
Mà \(\widehat {OAB} = \widehat {O{\rm{D}}C}\) nên \(\widehat{ABO}=\widehat{OAB}\) suy ra tam giác AOB cân tại O.
Vì tam giác AOB cân tại O nên OA = OB.
Mà hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường nên AC = BD.
Suy ra ABCD có hai đường chéo AC = BD nên ABCD là hình chữ nhật.
Video hướng dẫn giải
a) Cho hình bình hành ABCD có \(\widehat A = {90^o}\). ABCD có phải là hình chữ nhật hay không?
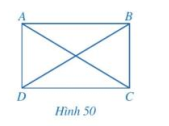
b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50)
Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh \(\widehat {ABC}\) và \(\widehat {DCB}\).
ABCD có phải là hình chữ nhật hay không?
Phương pháp giải:
Vận dụng các tính chất của hình bình hành
Lời giải chi tiết:
a) Hình bình hành ABCD có \(\widehat A = {90^o}\)
Suy ra: \(\widehat C = \widehat A = {90^o}\)
Suy ra: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{90}^o} - {{90}^o}}}{2} = {90^o}\)
Vậy ABCD là hình chữ nhật
b) Xét hai tam giác ABC và tam giác DCB có:
BC chung
AB = DC
AC = BD
Suy ra: \(\Delta ABC = \Delta DCB \Rightarrow \widehat {ABC} = \widehat {DCB}\)
Suy ra: \(\widehat {ABC} = \widehat {DCB} = \widehat {ADC} = \widehat {DAB} = {360^o}:4 = {90^o}\)
Vậy ABCD là hình chữ nhật.
Video hướng dẫn giải
a) Cho hình bình hành ABCD có \(\widehat A = {90^o}\). ABCD có phải là hình chữ nhật hay không?
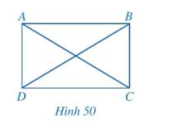
b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50)
Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh \(\widehat {ABC}\) và \(\widehat {DCB}\).
ABCD có phải là hình chữ nhật hay không?
Phương pháp giải:
Vận dụng các tính chất của hình bình hành
Lời giải chi tiết:
a) Hình bình hành ABCD có \(\widehat A = {90^o}\)
Suy ra: \(\widehat C = \widehat A = {90^o}\)
Suy ra: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{90}^o} - {{90}^o}}}{2} = {90^o}\)
Vậy ABCD là hình chữ nhật
b) Xét hai tam giác ABC và tam giác DCB có:
BC chung
AB = DC
AC = BD
Suy ra: \(\Delta ABC = \Delta DCB \Rightarrow \widehat {ABC} = \widehat {DCB}\)
Suy ra: \(\widehat {ABC} = \widehat {DCB} = \widehat {ADC} = \widehat {DAB} = {360^o}:4 = {90^o}\)
Vậy ABCD là hình chữ nhật.
Video hướng dẫn giải
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn \(\widehat {OAB} = \widehat {O{\rm{D}}C}\). Chứng minh ABCD là hình chữ nhật.
Phương pháp giải:
Chứng minh hình bình hành ABCD có AC = BD.
Lời giải chi tiết:
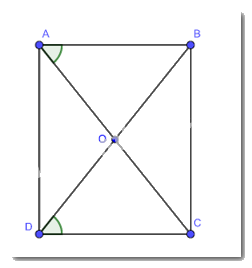
Do ABCD là hình bình hành suy ra AB = CD và AB // CD nên \(\widehat{ABO}=\widehat{ODC}\) (hai góc so le trong\)
Mà \(\widehat {OAB} = \widehat {O{\rm{D}}C}\) nên \(\widehat{ABO}=\widehat{OAB}\) suy ra tam giác AOB cân tại O.
Vì tam giác AOB cân tại O nên OA = OB.
Mà hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường nên AC = BD.
Suy ra ABCD có hai đường chéo AC = BD nên ABCD là hình chữ nhật.
Mục 3 trong SGK Toán 8 tập 1 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về hình học, cụ thể là các kiến thức liên quan đến tứ giác. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Mục 3 bao gồm các bài tập từ 1 đến 6, mỗi bài tập lại có những yêu cầu và độ khó khác nhau. Dưới đây là nội dung chi tiết và lời giải cho từng bài tập:
Bài 1 yêu cầu học sinh nhắc lại các loại tứ giác đã học (hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông) và các tính chất đặc trưng của từng loại. Đây là bài tập ôn tập kiến thức cơ bản, giúp học sinh hệ thống lại những gì đã học.
Bài 2 tập trung vào việc vận dụng các tính chất của hình bình hành để giải quyết các bài toán liên quan đến góc, cạnh, đường chéo. Học sinh cần nắm vững các tính chất như: các cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Bài 3 yêu cầu học sinh vận dụng các tính chất của hình chữ nhật để giải quyết các bài toán liên quan đến góc, cạnh, đường chéo. Học sinh cần nhớ rằng hình chữ nhật là một hình bình hành đặc biệt có bốn góc vuông và hai đường chéo bằng nhau.
Bài 4 tập trung vào việc vận dụng các tính chất của hình thoi để giải quyết các bài toán liên quan đến góc, cạnh, đường chéo. Học sinh cần nhớ rằng hình thoi là một hình bình hành đặc biệt có bốn cạnh bằng nhau và hai đường chéo vuông góc với nhau.
Bài 5 yêu cầu học sinh vận dụng các tính chất của hình vuông để giải quyết các bài toán liên quan đến góc, cạnh, đường chéo. Học sinh cần nhớ rằng hình vuông là một hình chữ nhật đặc biệt có bốn cạnh bằng nhau hoặc là một hình thoi đặc biệt có bốn góc vuông.
Bài 6 là một bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức về tất cả các loại tứ giác đã học để giải quyết một bài toán phức tạp hơn. Đây là bài tập giúp học sinh rèn luyện khả năng tư duy và giải quyết vấn đề một cách linh hoạt.
Kiến thức về tứ giác là nền tảng quan trọng cho việc học các kiến thức hình học nâng cao hơn trong chương trình Toán học. Việc nắm vững các định lý, tính chất của các loại tứ giác sẽ giúp học sinh giải quyết các bài toán một cách dễ dàng và hiệu quả hơn. Ngoài ra, kiến thức về tứ giác còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau của đời sống.
Hy vọng rằng bài giải chi tiết mục 3 trang 110, 111 SGK Toán 8 tập 1 - Cánh diều trên giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về các kiến thức về tứ giác và tự tin hơn trong quá trình học tập. Chúc các em học tốt!