Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 102, 103 sách giáo khoa Toán 8 tập 1 chương trình Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Quan sát hình thang ABCD (AB //CD, AB < CD) có hai đường chéo AC và BD bằng nhau kẻ BE song song với AC (E thuộc đường thẳng CD) như hình 27 a) Hai tam giác ABC và ECB có bằng nhau hay không? b) So sánh các cặp góc: (widehat {BE{rm{D}}}) và (widehat {B{rm{D}}E};widehat {AC{rm{D}}}) và (widehat {BE{rm{D}}}) c) Hai tam giác ACD và BDC có bằng nhau không? Từ đó, hãy so sánh (widehat {A{rm{D}}C}) và (widehat {BC{rm{D}}}). d) ABCD có phải là hình thang cân hay không?
Video hướng dẫn giải
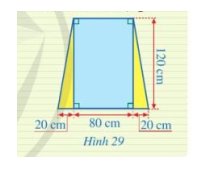
Một ô cửa sổ có dạng hình chữ nhật với chiều dài là 120 m và chiều rộng là 80 cm. Người ta mở rộng ô cửa sổ đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô của sổ đó có dạng hình gì? Tính diện tích của ô của sổ đó sau khi mở rộng.
Phương pháp giải:
Quan sát hình 29 sau khi mở rộng thì ô cửa đó có dạng hình thang cân.
Lời giải chi tiết:
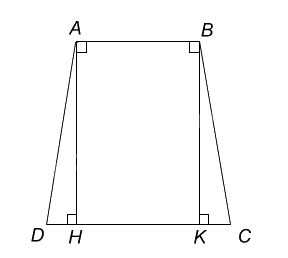
Xét \(\Delta AHD\) và \( \Delta BKC\) có:
\(\widehat {AHD} =\widehat{BKC} = 90^0\)
AH = BK
HD = KC
\( \Rightarrow \Delta AHD = \Delta BKC (c.g.c) \Rightarrow \widehat{ADH} = \widehat{BCK}\)
Do AB // KH hay AB // CD suy ra ABCD là hình thang.
Mà \(\widehat{ADH} = \widehat{BCK}\) (cmt)
Suy ra ABCD là hình thang cân.
Ta có: AB = HK = 80 (cm)
DC = DH + HK + KC = 20 + 80 + 20 = 120 (cm).
Chiều cao của hình thang ABCD là 120 cm (= BK).
=> Diện tích của ô cửa sổ sau khi mở rộng là:
\( S = \frac{1}{2}(AB + CD).BK = \frac{1}{2}(80 + 120).120 = 12000(cm^2)\)
Video hướng dẫn giải
Quan sát hình thang ABCD (AB //CD, AB < CD) có hai đường chéo AC và BD bằng nhau kẻ BE song song với AC (E thuộc đường thẳng CD) như hình 27
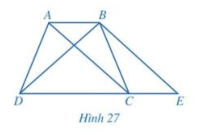
a) Hai tam giác ABC và ECB có bằng nhau hay không?
b) So sánh các cặp góc: \(\widehat {BE{\rm{D}}}\) và \(\widehat {B{\rm{D}}E};\widehat {AC{\rm{D}}}\) và \(\widehat {BE{\rm{D}}}\)
c) Hai tam giác ACD và BDC có bằng nhau không? Từ đó, hãy so sánh \(\widehat {A{\rm{D}}C}\) và \(\widehat {BC{\rm{D}}}\).
d) ABCD có phải là hình thang cân hay không?
Phương pháp giải:
a, chứng minh \(\Delta ABC = \Delta ECB(g.c.g)\)
b, \(\widehat {BED} = \widehat {BAC} = \widehat {BDE}\)
Lời giải chi tiết:
Do ABCD là hình thang nên AB//CD.
Kẻ BE//AC, \(E \in CD\) nên CE//AB.
\( \Rightarrow \widehat {BCE} = \widehat {ABC}\); \(\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong).
a, Xét \(\Delta ABC\)và \(\Delta ECB\) có:
\(\widehat {BCE} = \widehat {ABC}\)
BC chung
\(\widehat {CBE} = \widehat {ACB}\) (do BC//AC )
\( \Rightarrow \Delta ABC = \Delta ECB\)(g.c.g)
b, BE = AC = BD
\( \Rightarrow \Delta BDE\)cân tại B
\( \Rightarrow \widehat {BDE} = \widehat {BED}\)
Do \(\Delta ABC = \Delta ECB\)
\( \Rightarrow \widehat {BEC} = \widehat {BAC}\) (2 góc tương ứng) hay \(\widehat {BED} = \widehat {BAC}(1)\)
Mà: \(\widehat {BAC} = \widehat {ACD}\) (do AB//CD) (2)
Từ (1), (2) suy ra: \(\widehat {BED} = \widehat {ACD}\)
c, Theo câu b:
\(\begin{array}{l}\widehat {BED} = \widehat {BDE}\\\widehat {ACD} = \widehat {BED}\end{array}\) suy ra: \(\widehat {ACD} = \widehat {BDE}\) hay \(\widehat {ACD} = \widehat {BDC}\)
Xét \(\Delta ACD\)và \(\Delta BDC\)có:
CD chung
\(\widehat {ACD} = \widehat {BDC}\)
AC = BD (gt)
\( \Rightarrow \Delta ACD = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (2 góc tương ứng)
d, Hình thang ABCD (AB//CD) có \(\widehat {ADC} = \widehat {BCD}\)nên hình thang ABCD là hình thang cân.
Video hướng dẫn giải
Một ô cửa sổ có dạng hình chữ nhật với chiều dài là 120 m và chiều rộng là 80 cm. Người ta mở rộng ô cửa sổ đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô của sổ đó có dạng hình gì? Tính diện tích của ô của sổ đó sau khi mở rộng.
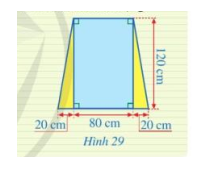
Phương pháp giải:
Quan sát hình 29 sau khi mở rộng thì ô cửa đó có dạng hình thang cân.
Lời giải chi tiết:
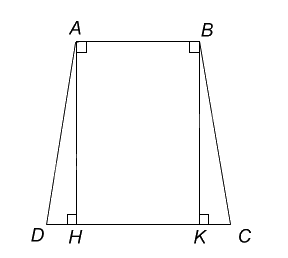
Xét \(\Delta AHD\) và \( \Delta BKC\) có:
\(\widehat {AHD} =\widehat{BKC} = 90^0\)
AH = BK
HD = KC
\( \Rightarrow \Delta AHD = \Delta BKC (c.g.c) \Rightarrow \widehat{ADH} = \widehat{BCK}\)
Do AB // KH hay AB // CD suy ra ABCD là hình thang.
Mà \(\widehat{ADH} = \widehat{BCK}\) (cmt)
Suy ra ABCD là hình thang cân.
Ta có: AB = HK = 80 (cm)
DC = DH + HK + KC = 20 + 80 + 20 = 120 (cm).
Chiều cao của hình thang ABCD là 120 cm (= BK).
=> Diện tích của ô cửa sổ sau khi mở rộng là:
\( S = \frac{1}{2}(AB + CD).BK = \frac{1}{2}(80 + 120).120 = 12000(cm^2)\)
Video hướng dẫn giải
Quan sát hình thang ABCD (AB //CD, AB < CD) có hai đường chéo AC và BD bằng nhau kẻ BE song song với AC (E thuộc đường thẳng CD) như hình 27
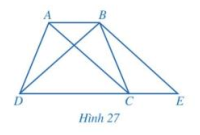
a) Hai tam giác ABC và ECB có bằng nhau hay không?
b) So sánh các cặp góc: \(\widehat {BE{\rm{D}}}\) và \(\widehat {B{\rm{D}}E};\widehat {AC{\rm{D}}}\) và \(\widehat {BE{\rm{D}}}\)
c) Hai tam giác ACD và BDC có bằng nhau không? Từ đó, hãy so sánh \(\widehat {A{\rm{D}}C}\) và \(\widehat {BC{\rm{D}}}\).
d) ABCD có phải là hình thang cân hay không?
Phương pháp giải:
a, chứng minh \(\Delta ABC = \Delta ECB(g.c.g)\)
b, \(\widehat {BED} = \widehat {BAC} = \widehat {BDE}\)
Lời giải chi tiết:
Do ABCD là hình thang nên AB//CD.
Kẻ BE//AC, \(E \in CD\) nên CE//AB.
\( \Rightarrow \widehat {BCE} = \widehat {ABC}\); \(\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong).
a, Xét \(\Delta ABC\)và \(\Delta ECB\) có:
\(\widehat {BCE} = \widehat {ABC}\)
BC chung
\(\widehat {CBE} = \widehat {ACB}\) (do BC//AC )
\( \Rightarrow \Delta ABC = \Delta ECB\)(g.c.g)
b, BE = AC = BD
\( \Rightarrow \Delta BDE\)cân tại B
\( \Rightarrow \widehat {BDE} = \widehat {BED}\)
Do \(\Delta ABC = \Delta ECB\)
\( \Rightarrow \widehat {BEC} = \widehat {BAC}\) (2 góc tương ứng) hay \(\widehat {BED} = \widehat {BAC}(1)\)
Mà: \(\widehat {BAC} = \widehat {ACD}\) (do AB//CD) (2)
Từ (1), (2) suy ra: \(\widehat {BED} = \widehat {ACD}\)
c, Theo câu b:
\(\begin{array}{l}\widehat {BED} = \widehat {BDE}\\\widehat {ACD} = \widehat {BED}\end{array}\) suy ra: \(\widehat {ACD} = \widehat {BDE}\) hay \(\widehat {ACD} = \widehat {BDC}\)
Xét \(\Delta ACD\)và \(\Delta BDC\)có:
CD chung
\(\widehat {ACD} = \widehat {BDC}\)
AC = BD (gt)
\( \Rightarrow \Delta ACD = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (2 góc tương ứng)
d, Hình thang ABCD (AB//CD) có \(\widehat {ADC} = \widehat {BCD}\)nên hình thang ABCD là hình thang cân.
Mục 3 trong SGK Toán 8 tập 1 chương trình Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các công thức, quy tắc đã học để thực hiện các phép toán, chứng minh đẳng thức, giải phương trình và bài toán thực tế.
Bài 1 yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia đa thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu, bậc của đa thức và các công thức biến đổi đa thức.
Bài 2 tập trung vào việc rút gọn phân thức, quy đồng mẫu số, cộng trừ phân thức. Học sinh cần nhớ các quy tắc về mẫu số chung, điều kiện xác định của phân thức và các công thức biến đổi phân thức.
Bài 3 là một bài tập tổng hợp, yêu cầu học sinh vận dụng tất cả các kiến thức đã học trong mục 3 để giải quyết các bài toán phức tạp hơn. Bài tập này thường có tính ứng dụng cao, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong mục 3 trang 102, 103 SGK Toán 8 tập 1 - Cánh diều. Các lời giải được trình bày một cách logic, rõ ràng, giúp học sinh dễ dàng theo dõi và hiểu được phương pháp giải.
Ngoài ra, chúng tôi còn cung cấp các hướng dẫn giải bài tập, các lưu ý quan trọng và các bài tập tương tự để học sinh có thể tự luyện tập và củng cố kiến thức.
Việc giải bài tập là một phần không thể thiếu trong quá trình học tập môn Toán. Giải bài tập giúp học sinh:
Để giải bài tập Toán 8 hiệu quả, học sinh nên:
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập tại giaitoan.edu.vn, các em học sinh sẽ học tập tốt môn Toán 8 và đạt được kết quả cao trong học tập. Chúc các em thành công!
| Bài tập | Lời giải |
|---|---|
| Bài 1a | Xem lời giải |
| Bài 2b | Xem lời giải |