Chào mừng bạn đến với bài học về Lý thuyết Mặt phẳng tọa độ và Đồ thị của hàm số trong chương trình Toán 8 - Cánh diều tại giaitoan.edu.vn.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về hệ tọa độ, cách biểu diễn điểm trên mặt phẳng tọa độ, và đặc biệt là cách vẽ đồ thị của hàm số bậc nhất.
Mặt phẳng tọa độ là gì?
1. Mặt phẳng tọa độ
Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó ta có trục tọa độ Oxy.
Trục Ox, Oy gọi là các trục tọa độ. Ox là trục hoành, Oy là trục tung. O là gốc tọa độ.
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng Oxy.
Chú ý. Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau.
2. Tọa độ của một điểm trong mặt phẳng tọa độ
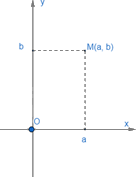
Cho điểm M nằm trong mặt phẳng tọa độ.
Giả sử hình chiếu của điểm M lên Ox là điểm a, lên Oy là điểm b. Cặp số (a;b) gọi là tọa độ của điểm M, a là hoành độ, b là tung độ.
Điểm M có tọa độ (a; b) kí hiệu là M(a; b).
3. Độ thị của hàm số
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x;f(x)) trên mặt phẳng tọa độ.
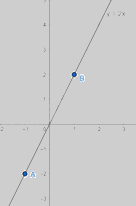
Ví dụ: Xét hàm số y = 2x
Giá trị \({y_1};{y_2}\) tương ứng với \({x_1} = - 1;{x_2} = 1\) là: \({y_1} = 2.( - 1) = - 2;\,\,y_2^{} = 2.1 = 2\)
Hàm số y = 2x có đồ thị như sau:
Mặt phẳng tọa độ là nền tảng quan trọng trong hình học giải tích và đại số. Việc nắm vững lý thuyết và kỹ năng vẽ đồ thị hàm số là điều cần thiết để giải quyết các bài toán liên quan đến hàm số bậc nhất và các bài toán thực tế.
Hệ tọa độ Descartes (hay còn gọi là hệ tọa độ vuông góc) bao gồm hai trục vuông góc nhau: trục hoành (Ox) và trục tung (Oy). Giao điểm của hai trục này là gốc tọa độ (O). Mỗi điểm trên mặt phẳng tọa độ được xác định bởi một cặp số (x, y) gọi là tọa độ của điểm đó. x là hoành độ, y là tung độ.
Để biểu diễn một điểm A(x, y) trên mặt phẳng tọa độ, ta thực hiện các bước sau:
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. Hệ số a được gọi là hệ số góc của đường thẳng, b là tung độ gốc.
Đồ thị của hàm số y = ax + b là một đường thẳng.
Để vẽ đồ thị của hàm số y = ax + b, ta thực hiện các bước sau:
Vẽ đồ thị của hàm số y = 2x - 1.
Bước 1: Xác định hai điểm thuộc đồ thị.
Bước 2: Vẽ đường thẳng đi qua hai điểm A(0, -1) và B(1, 1).
Hãy vẽ đồ thị của các hàm số sau:
Khi vẽ đồ thị hàm số, cần chú ý đến hệ số góc a để xác định chiều của đường thẳng. Ngoài ra, cần kiểm tra lại các điểm đã xác định để đảm bảo tính chính xác của đồ thị.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Mặt phẳng tọa độ và Đồ thị của hàm số trong chương trình Toán 8 - Cánh diều. Chúc bạn học tập tốt!