Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 115 SGK Toán 8 tập 1 - Cánh diều. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho hình thoi ABCD có
Đề bài
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:
\(A{C^2} + B{{\rm{D}}^2} = 4\left( {O{A^2} + O{B^2}} \right) = 4{\rm{A}}{B^2}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pythagore trong các tam giác vuông để chứng minh.
Lời giải chi tiết
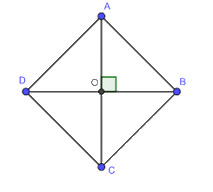
Xét \(\Delta OAB\) vuông tại A có: \(O{A^2} + O{B^2} = A{B^2}\)
Vì ABCD là hình thoi nên OA = OC; OB = OD
Ta có:
\(\begin{array}{l}A{C^2} + B{D^2} = {(OA + OC)^2} + {(OB + OD)^2}\\ = {(OA + OA)^2} + {(OB + OB)^2}\\ = {(2OA)^2} + {(2OB)^2} = 4.O{A^2} + 4.O{B^2} = 4{(OA^2 + OB^2)} = 4.A{B^2}\end{array}\)
Bài 2 trang 115 SGK Toán 8 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về hình bình hành, hình chữ nhật, hình thoi và hình vuông để giải quyết các bài toán liên quan đến tính chất đường chéo, diện tích và các yếu tố khác của các hình này.
Để giải bài 2 trang 115 SGK Toán 8 tập 1 - Cánh diều một cách hiệu quả, các em cần:
Bài 2: (Đề bài cụ thể của bài 2 sẽ được trình bày tại đây. Ví dụ: Cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Biết AB = 5cm, BC = 8cm, góc ABC = 60 độ. Tính độ dài AC và BD.)
(Giải chi tiết từng bước của bài toán, sử dụng các công thức và tính chất đã nêu ở trên. Ví dụ:)
Áp dụng định lý cosin trong tam giác ABC, ta có:
AC2 = AB2 + BC2 - 2.AB.BC.cos(ABC)
AC2 = 52 + 82 - 2.5.8.cos(60o)
AC2 = 25 + 64 - 80.0.5
AC2 = 49
AC = 7cm
...
AC = 7cm (hoặc kết quả cụ thể của bài toán)
Để củng cố kiến thức và kỹ năng giải bài tập về hình học, các em có thể tham khảo thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể luyện tập thêm trên các trang web học toán online uy tín.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em sẽ học tập tốt môn Toán 8 và đạt kết quả cao trong các kỳ thi.