Lý Thuyết Đồ Thị Hàm Số Bậc Nhất y = ax + b (a ≠ 0) Toán 8 Cánh Diều

Lý thuyết Đồ thị hàm số bậc nhất y = ax + b ( a ≠ 0) SGK Toán 8 - Cánh diều

Lý Thuyết Đồ Thị Hàm Số Bậc Nhất y = ax + b (a ≠ 0) - Toán 8 Cánh Diều

Bài viết này cung cấp đầy đủ và chi tiết lý thuyết về đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) theo chương trình SGK Toán 8 Cánh Diều. Chúng tôi sẽ giúp bạn hiểu rõ các khái niệm, tính chất và cách vẽ đồ thị hàm số một cách dễ dàng.

Với phương pháp trình bày trực quan, dễ hiểu, cùng với các ví dụ minh họa cụ thể, bạn sẽ nắm vững kiến thức và tự tin giải các bài tập liên quan đến hàm số bậc nhất.

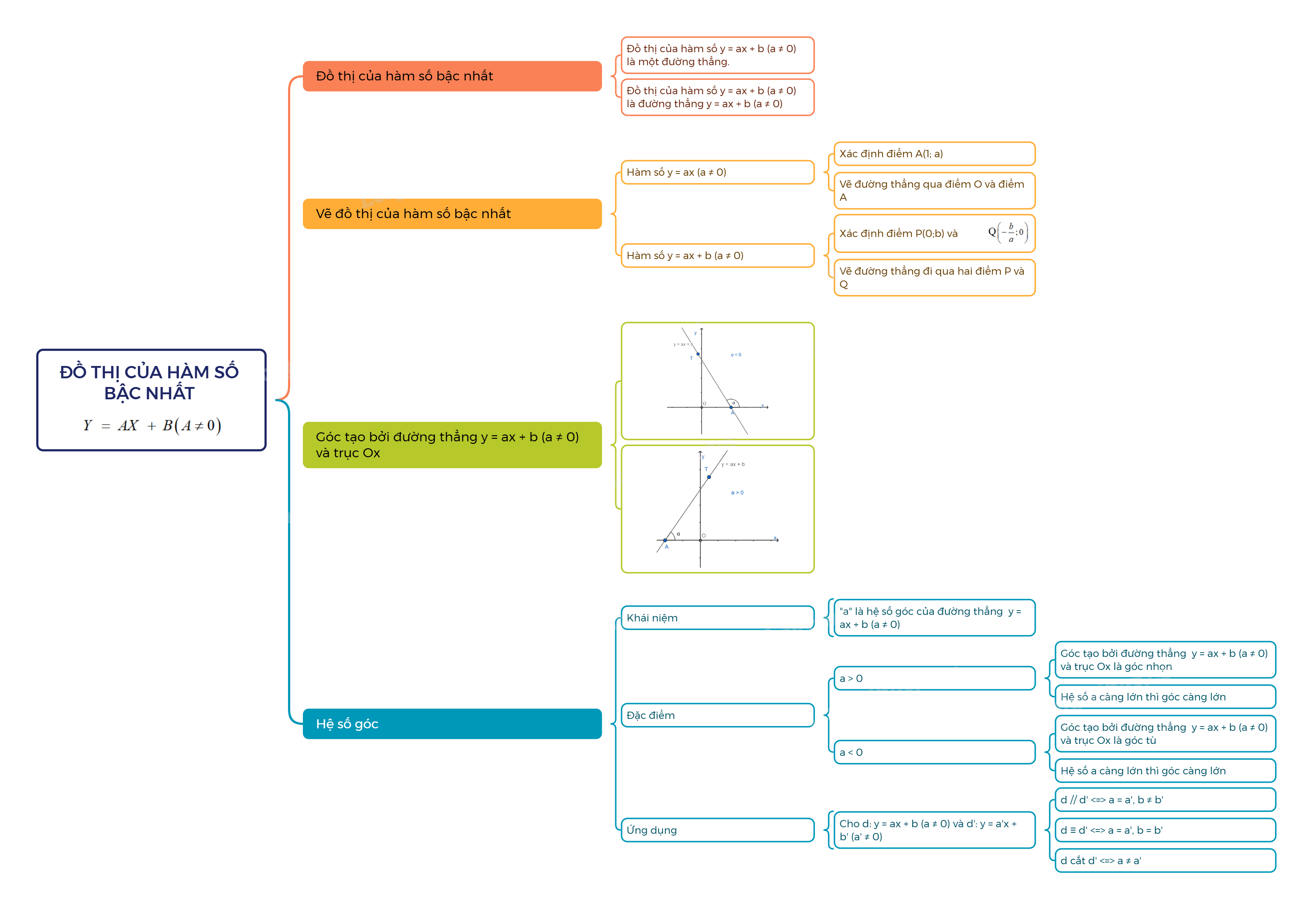
Đồ thị của hàm số bậc nhất là gì?

1. Đồ thị của hàm số bậc nhất

Đồ thị của hàm số y = ax + b (a\( \ne \)0) là một đường thẳng.

Chú ý: Đồ thị hàm số y = ax + b (a\( \ne \)0) còn gọi là đường thẳng y = ax + b (a\( \ne \)0).

Ví dụ: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3.

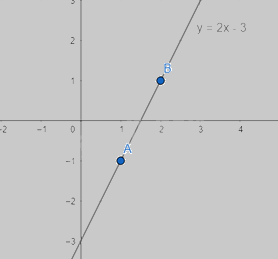
Lý thuyết Đồ thị hàm số bậc nhất y = ax + b ( a ≠ 0) SGK Toán 8 - Cánh diều 1

2. Vẽ đồ thị của hàm số bậc nhất

Hàm số y = ax (a\( \ne \)0)

Để vẽ đồ thị của hàm số y = ax (a\( \ne \)0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.

Hàm số y = ax + b (a\( \ne \)0)

Để vẽ đồ thị của hàm số y = ax + b (a\( \ne \)0, b\( \ne \)0), ta có thể xác định hai điểm P(0; b) và Q\(\left( { - \frac{b}{a};0} \right)\) rồi vẽ dường thẳng đi qua hai điểm đó.

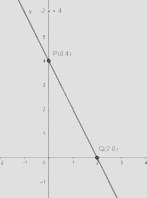
Ví dụ: Cho hàm số y = -2x + 4

Với x = 0 thì y = 4, ta được điểm P(0;4)

Với y = 0 thì x = 2, ta được điểm Q(2;0)

Vậy đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)

Lý thuyết Đồ thị hàm số bậc nhất y = ax + b ( a ≠ 0) SGK Toán 8 - Cánh diều 2

3. Hệ số góc của đường thẳng y = ax + b (a\( \ne \)0)

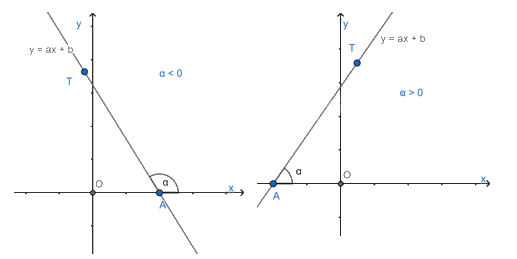
Góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox.

Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a\( \ne \)0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.

Góc \(\alpha \) tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc \(\alpha \))

Lý thuyết Đồ thị hàm số bậc nhất y = ax + b ( a ≠ 0) SGK Toán 8 - Cánh diều 3

Hệ số góc

Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a\( \ne \)0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a\( \ne \)0).

Nhận xét:

Khi hệ số góc a > 0 thì góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.

Khi hệ số góc a < 0 thì góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.

Ứng dụng của hệ số góc

Cho d: y = ax + b (a\( \ne \)0) và d’: y = a’x + b’ (a’\( \ne \)0)

a. d // d’ \( \Leftrightarrow \) a = a’, b \( \ne \)b’.

b.\(d \equiv d' \Leftrightarrow a = a',b = b'\)

c. d cắt d’ \( \Leftrightarrow \) a \( \ne \)a’

Ví dụ: y = 2x + 1, y = 2x + 3 là hai đường thẳng song song vì có hệ số góc bằng nhau và hệ số tự do khác nhau.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Lý thuyết Đồ thị hàm số bậc nhất y = ax + b ( a ≠ 0) SGK Toán 8 - Cánh diều đặc sắc thuộc chuyên mục bài tập sách giáo khoa toán 8 trên môn toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Lý Thuyết Đồ Thị Hàm Số Bậc Nhất y = ax + b (a ≠ 0) - Toán 8 Cánh Diều

Hàm số bậc nhất là một trong những khái niệm cơ bản và quan trọng trong chương trình Toán học lớp 8. Việc nắm vững lý thuyết và kỹ năng vẽ đồ thị hàm số bậc nhất là nền tảng để học tốt các kiến thức toán học nâng cao hơn.

1. Định nghĩa Hàm Số Bậc Nhất

Hàm số bậc nhất là hàm số có dạng y = ax + b, trong đó:

x là biến độc lập.
y là biến phụ thuộc.
a và b là các số thực, với a ≠ 0.

Hệ số a được gọi là hệ số góc, và b được gọi là tung độ gốc.

2. Ý Nghĩa của Hệ Số a

Hệ số a quyết định độ dốc của đường thẳng biểu diễn hàm số. Cụ thể:

Nếu a > 0: Đường thẳng đi lên từ trái sang phải.
Nếu a < 0: Đường thẳng đi xuống từ trái sang phải.
Độ lớn của |a| càng lớn, đường thẳng càng dốc.

3. Ý Nghĩa của Hệ Số b

Hệ số b là tung độ gốc, tức là tọa độ giao điểm của đường thẳng với trục Oy. Khi x = 0, y = b.

4. Cách Vẽ Đồ Thị Hàm Số Bậc Nhất y = ax + b

Để vẽ đồ thị hàm số y = ax + b, ta thực hiện các bước sau:

Xác định hai điểm thuộc đồ thị. Thông thường, ta chọn x = 0 để tìm y = b (điểm A(0, b)) và chọn một giá trị x khác để tính y tương ứng (điểm B(x₁, y₁)).
Vẽ đường thẳng đi qua hai điểm A và B.

Ví dụ: Vẽ đồ thị hàm số y = 2x + 1

Chọn x = 0, ta có y = 2(0) + 1 = 1. Vậy điểm A(0, 1) thuộc đồ thị.
Chọn x = 1, ta có y = 2(1) + 1 = 3. Vậy điểm B(1, 3) thuộc đồ thị.
Vẽ đường thẳng đi qua hai điểm A(0, 1) và B(1, 3).

5. Các Trường Hợp Đặc Biệt

Nếu a = 0: Hàm số trở thành y = b, là hàm số hằng. Đồ thị là một đường thẳng nằm ngang cắt trục Oy tại điểm (0, b).
Nếu b = 0: Hàm số trở thành y = ax, là hàm số đi qua gốc tọa độ O(0, 0).

6. Bài Tập Vận Dụng

Bài 1: Vẽ đồ thị hàm số y = -x + 2

Bài 2: Xác định hệ số a và b của hàm số có đồ thị đi qua các điểm A(1, 3) và B(-1, 1)

Bài 3: Tìm giao điểm của hai đường thẳng y = 2x - 1 và y = -x + 2

7. Ứng Dụng của Hàm Số Bậc Nhất

Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ:

Tính quãng đường đi được của một vật chuyển động đều.
Tính tiền lương dựa trên số giờ làm việc.
Biểu diễn mối quan hệ giữa nhiệt độ và thời gian.

Việc hiểu rõ lý thuyết và kỹ năng vẽ đồ thị hàm số bậc nhất sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả.

8. Tổng Kết

Bài viết này đã trình bày đầy đủ và chi tiết lý thuyết về đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) SGK Toán 8 Cánh Diều. Hy vọng rằng, với những kiến thức này, bạn sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến hàm số bậc nhất.