Bài 2 trang 57 SGK Toán 8 – Cánh diều là một bài tập quan trọng trong chương trình học Toán 8, giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong SGK Toán 8 – Cánh diều, giúp các em học sinh có thể tự học và ôn tập hiệu quả.
Cho hình thang ABCD
Đề bài
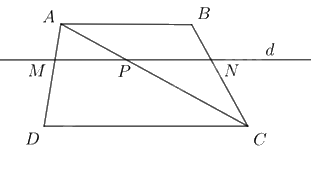
Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\) có AB = 4cm, CD = 6cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào hệ quả của định lý Thales để tính độ dài đoạn thẳng AN.
Lời giải chi tiết
a) Vì \(d\parallel CD\) nên \(MP\parallel CD\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{MD}} = \frac{{AP}}{{PC}}\,\,\left( 1 \right)\) (Định lý Thales)
Vì \(d\parallel AB\) nên \(PN\parallel AB\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{BN}}{{NC}} = \frac{{AP}}{{PC}}\,\,\left( 2 \right)\) (Định lý Thales)
Từ (1) và (2) ta có \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\).
b) Vì \(MD = 2MA\) nên \(\frac{{AM}}{{MD}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AD}} = \frac{1}{3}\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{AD}} = \frac{{MP}}{{DC}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{MP}}{{DC}} = \frac{1}{3} \Rightarrow MP = \frac{1}{3}DC = 2cm\)
Vì \(\frac{{AM}}{{AD}} = \frac{1}{3} \Rightarrow \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow \frac{{PC}}{{CA}} = \frac{2}{3}\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{CP}}{{CA}} = \frac{{PN}}{{AB}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{PN}}{{AB}} = \frac{2}{3} \Rightarrow PN = \frac{2}{3}AB = \frac{8}{3}cm\)
Mà \(MN = MP + PM = 2 + \frac{8}{3} = \frac{{14}}{3}cm\).
Bài 2 trang 57 SGK Toán 8 – Cánh diều thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 2 trang 57 SGK Toán 8 – Cánh diều thường yêu cầu học sinh chứng minh một tứ giác là hình thang cân, tính độ dài các cạnh hoặc góc, hoặc tìm mối liên hệ giữa các yếu tố của hình thang cân. Để giải bài tập này, học sinh cần:
Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng EA = EB.
Lời giải:
Để củng cố kiến thức về hình thang cân, học sinh có thể làm thêm các bài tập tương tự như:
Khi giải bài tập về hình thang cân, học sinh cần lưu ý:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và đáp án cho học sinh các cấp. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em học toán hiệu quả và đạt kết quả cao.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài 2 trang 57 SGK Toán 8 – Cánh diều trên đây, các em học sinh sẽ hiểu rõ hơn về kiến thức về hình thang cân và có thể tự tin giải các bài tập tương tự. Chúc các em học tập tốt!