Chào mừng bạn đến với bài học lý thuyết quan trọng về Đơn thức nhiều biến và Đa thức nhiều biến trong chương trình Toán 8, sách Cánh Diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản, định nghĩa, tính chất và các quy tắc quan trọng để giải quyết các bài toán liên quan.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn trải nghiệm học tập trực tuyến hiệu quả và thú vị. Hãy cùng bắt đầu khám phá thế giới của Đơn thức và Đa thức nhiều biến!
Đơn thức nhiều biến là gì?
Đơn thức nhiều biến (hay đơn thức) là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và các biến.
Số 0 được gọi là đơn thức không.
Ví dụ: \(1;2xy; - \frac{3}{4}{x^2}y( - 4x);...\) là các đơn thức.
Đơn thức thu gọn là đơn thức chỉ gồm một số với các biến, mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương và chỉ được viết một lần.
Ví dụ:
\(1;2xy;5{x^2}{y^4}z;...\) là các đơn thức thu gọn.
\(3{x^2}yx; - \frac{3}{4}{x^2}y( - 4x);...\) không phải là các đơn thức thu gọn.
Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.
Ví dụ: đơn thức \(3{x^3}.y\) có hệ số là 3, phần biến là \({x^3}.y\).
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Ví dụ:
Hai đơn thức \(5{x^2}{y^4}z\) và \( - \frac{1}{3}{x^2}{y^4}z\) có hệ số khác 0 và có cùng phần biến nên chúng là hai đơn thức đồng dạng.
Hai đơn thức \(5{x^2}{y^4}z\) và \(5x{y^2}z\) không có cùng phần biến nên chúng không phải là hai đơn thức đồng dạng.
Cộng, trừ các đơn thức đồng dạng
Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.
Ví dụ:
\(\begin{array}{l}2{x^3}{y^2} + 4{x^3}{y^2} = 6{x^3}{y^2}\\4a{y^2} - 3a{y^2} = a{y^2}\end{array}\)
Đa thức nhiều biến (hay đa thức)là một tổng của những đơn thức.
Chú ý: Mỗi đơn thức được gọi là một đa thức.
Ví dụ: \({x^2} - 4x + 3;{x^2}\; + {\rm{ }}3xy{z^2}\; - {\rm{ }}yz{\rm{ }} + {\rm{ }}1;\left( {x{\rm{ }} + {\rm{ }}3y} \right){\rm{ }} + \left( {2x{\rm{ }}--{\rm{ }}y} \right)\) là đa thức.
\(\frac{{x + y}}{{x - y}},\frac{{{x^2} + 2}}{{{x^2} - {y^2}}}\) không phải là đa thức.
Thu gọn đa thức nhiều biến là làm cho trong đa thức đó không còn hai đơn thức nào đồng dạng.
Ví dụ:
\(\begin{array}{l}A = {x^3} - 2{x^2}y - {x^2}y + 3x{y^2} - {y^3}\\\,\,\,\,\, = {x^3} - 3{x^2}y - 3x{y^2} - {y^3}\end{array}\)
Tính giá trị của đa thức
Để tính giá trị của một đa thức tại những giá trị cho trước của các biến, ta thay những giá trị cho trước đó vào biểu thức xác định đa thức rồi thực hiện phép tính.
Ví dụ: Giá trị của biểu thức \({x^2} - 4xy + 3{y^2}\) tại x = 2, y = 1 là: \({2^2} - 4.2.1 + {3.1^2} = - 1\)
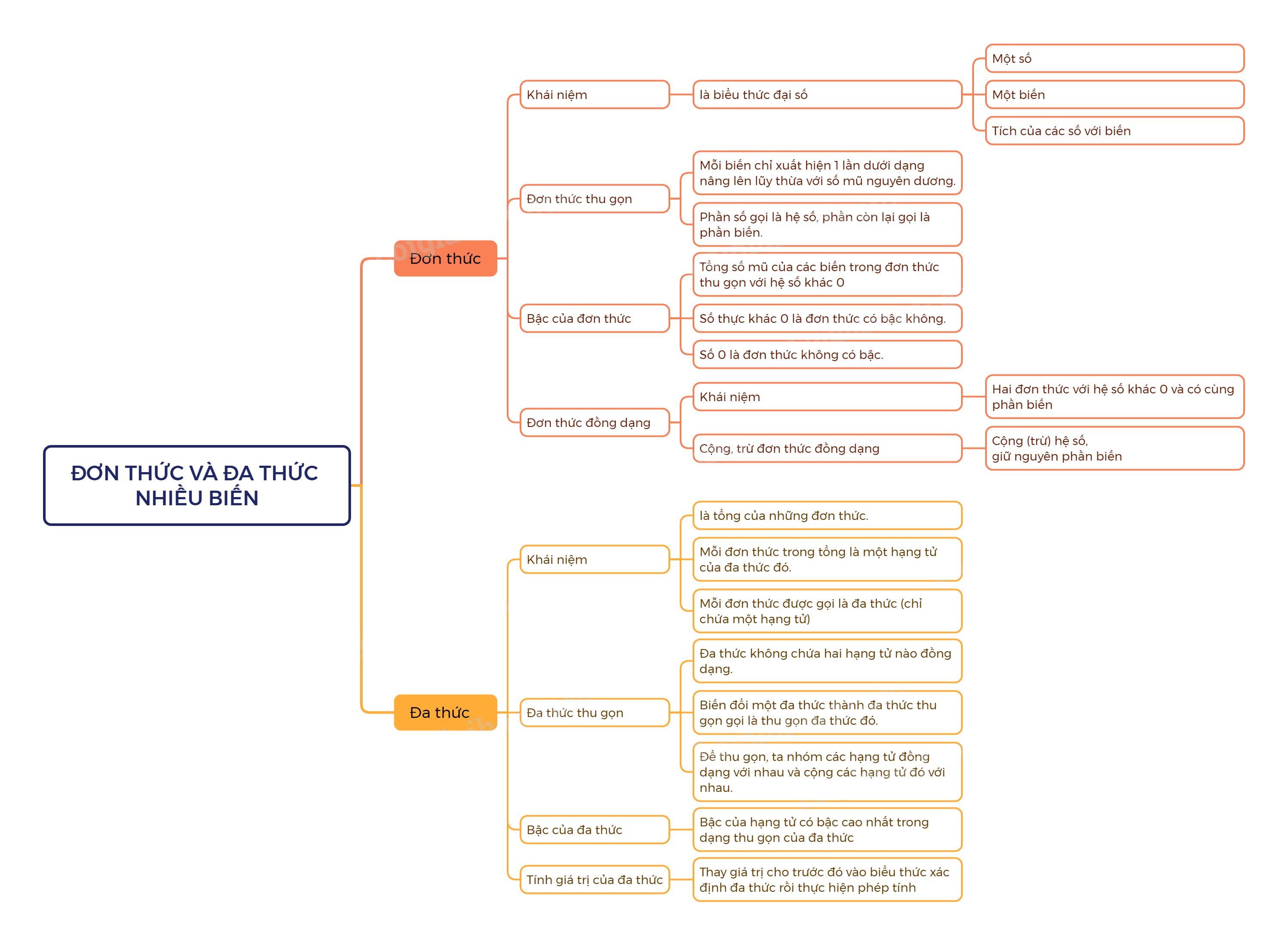
Bài học này sẽ đi sâu vào lý thuyết về đơn thức nhiều biến và đa thức nhiều biến, một trong những chủ đề quan trọng của chương trình Toán 8, sách Cánh Diều. Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các khái niệm liên quan, và các quy tắc để thực hiện các phép toán với đơn thức và đa thức.
Định nghĩa: Đơn thức nhiều biến là biểu thức đại số có dạng axmynzp..., trong đó a là hệ số, x, y, z,... là các biến, và m, n, p,... là các số tự nhiên.
Bậc của đơn thức: Bậc của đơn thức là tổng số mũ của các biến trong đơn thức.
Ví dụ:
Định nghĩa: Đa thức nhiều biến là tổng của các đơn thức nhiều biến.
Ví dụ:
2x2y + 3xy - 5x + 1 là một đa thức nhiều biến.
Phép cộng, trừ đơn thức đồng dạng: Để cộng hoặc trừ các đơn thức đồng dạng, ta cộng hoặc trừ các hệ số và giữ nguyên phần biến.
Ví dụ:
3x2y + 5x2y = 8x2y
Phép cộng, trừ đa thức: Để cộng hoặc trừ các đa thức, ta cộng hoặc trừ các đơn thức đồng dạng trong mỗi đa thức.
Phép nhân đa thức: Ta sử dụng tính chất phân phối để nhân đa thức với đa thức.
Ví dụ:
(x + 2)(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6
Dưới đây là một số bài tập để bạn luyện tập và củng cố kiến thức:
Hi vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết Đơn thức nhiều biến và Đa thức nhiều biến trong chương trình Toán 8, sách Cánh Diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!