Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 17 SGK Toán 8 tập 1 - Cánh diều. Bài học này thuộc chương trình đại số lớp 8, tập trung vào việc hiểu và vận dụng các kiến thức về đa thức.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
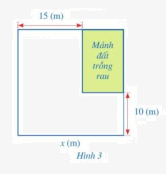
Khu vườn của nhà bác Xuân có dạng hình vuông. Bác Xuân muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn để trồng rau (hình 3). Biết diện tích của mảnh đất trồng rau bằng 150 m2. Tính độ dài cạnh x (m) của khu vườn đó.
Đề bài
Khu vườn của nhà bác Xuân có dạng hình vuông. Bác Xuân muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn để trồng rau (hình 3). Biết diện tích của mảnh đất không trồng rau bằng 475 m2. Tính độ dài cạnh x (m) của khu vườn đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Tính độ dài các cạnh mảnh đất hình chữ nhật để trồng rau là: x – 15 (m); x – 10 (m)
Diện tích mảnh đất trồng rau là: \(\left( {x - 15} \right).\left( {x - 10} \right) = {x^2} - 25{\rm{x}} + 150 \) (m2)
Vì diện tích của mảnh đất không trồng rau bằng 475 m2 nên tính được độ dài cạnh của khu vườn.
Lời giải chi tiết
Mảnh đất hình chữ nhật có độ dài lần lượt các cạnh là: x – 15 (m); x – 10 (m)
Diện tích mảnh đất trồng rau là: \(\left( {x - 15} \right).\left( {x - 10} \right) = {x^2} - 25{\rm{x}} + 150\) (m2)
Vì diện tích của mảnh đất không trồng rau bằng 475 m2 nên
\(\begin{array}{l}{x^2} - ({x^2} - 25{\rm{x}} + 150) = 475\\ \Leftrightarrow {x^2} - {x^2} + 25{\rm{x}} - 150 = 475\\ \Leftrightarrow 25x = 625\end{array}\)
Nên x = 25
Vì x là độ dài cạnh của khu vườn nên x = 25 m.
Bài 7 trang 17 SGK Toán 8 tập 1 - Cánh diều yêu cầu học sinh phân tích các đa thức thành nhân tử. Đây là một kỹ năng quan trọng trong đại số, giúp đơn giản hóa biểu thức và giải các phương trình bậc cao. Để giải bài tập này, chúng ta cần nắm vững các phương pháp phân tích đa thức thành nhân tử như đặt nhân tử chung, sử dụng hằng đẳng thức, và nhóm các số hạng.
Bài 7 bao gồm các câu hỏi yêu cầu phân tích đa thức sau thành nhân tử:
Đặt nhân tử chung 3x:
3x² - 6x = 3x(x - 2)
Sử dụng hằng đẳng thức (a - b)² = a² - 2ab + b²:
x² - 2x + 1 = (x - 1)²
Sử dụng hằng đẳng thức a³ + b³ = (a + b)(a² - ab + b²):
x³ + 8 = x³ + 2³ = (x + 2)(x² - 2x + 4)
Sử dụng hằng đẳng thức (a - b)² = a² - 2ab + b²:
x² - 4x + 4 = (x - 2)²
Sử dụng hằng đẳng thức a³ - b³ = (a - b)(a² + ab + b²):
x³ - 27 = x³ - 3³ = (x - 3)(x² + 3x + 9)
Sử dụng hằng đẳng thức (a + b)² = a² + 2ab + b²:
x² + 4x + 4 = (x + 2)²
Để hiểu rõ hơn về phương pháp phân tích đa thức thành nhân tử, chúng ta cùng xem xét một ví dụ khác:
Phân tích đa thức 2x² + 4x thành nhân tử.
Giải:
2x² + 4x = 2x(x + 2)
Việc phân tích đa thức thành nhân tử có nhiều ứng dụng trong toán học, bao gồm:
Để củng cố kiến thức về phân tích đa thức thành nhân tử, các em có thể tự giải các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ hiểu rõ hơn về cách giải bài 7 trang 17 SGK Toán 8 tập 1 - Cánh diều và tự tin hơn trong quá trình học tập môn Toán.