Bài học này sẽ cung cấp cho bạn kiến thức nền tảng về Trường hợp đồng dạng thứ hai của tam giác, một trong những tiêu chí quan trọng để xác định hai tam giác có đồng dạng hay không. Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện áp dụng và các ví dụ minh họa cụ thể.
Nội dung bài học được trình bày chi tiết, dễ hiểu, phù hợp với chương trình SGK Toán 8 - Cánh diều, giúp bạn tự tin giải các bài tập liên quan.
Trường hợp đồng dạng thứ hai của tam giác là gì?
1. Trường hợp đồng dạng thứ hai: Cạnh – góc – cạnh
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
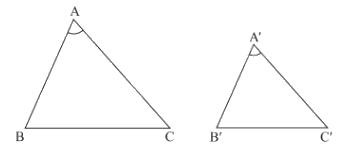
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}},\widehat {A'} = \widehat A\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,(c.g.c)\end{array}\)
2. Trường hợp đồng dạng thứ hai của tam giác vuông
Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
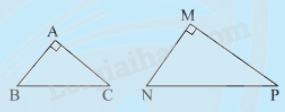
\(\Delta ABC,\Delta MNP,\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}},\widehat M = \widehat A = {90^0}\)
\( \Rightarrow \Delta MNP \backsim \Delta ABC\,\)(2cgv)
Trong chương trình Toán 8, việc nắm vững các trường hợp đồng dạng của tam giác là vô cùng quan trọng. Bài viết này sẽ đi sâu vào phân tích Lý thuyết Trường hợp đồng dạng thứ hai của tam giác theo chương trình SGK Toán 8 - Cánh diều, cung cấp kiến thức đầy đủ và dễ hiểu nhất cho học sinh.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Kí hiệu: ΔABC ~ ΔA'B'C' (đọc là tam giác ABC đồng dạng với tam giác A'B'C').
Định lý: Nếu một đường thẳng cắt hai cạnh của tam giác và tạo ra hai tam giác đồng dạng thì tam giác đó đồng dạng với tam giác còn lại.
Cụ thể, cho tam giác ABC, một đường thẳng d cắt AB tại M và AC tại N sao cho:
Khi đó, ΔAMN ~ ΔABC.
Chứng minh:
Vậy, ΔAMN ~ ΔABC (trường hợp góc - góc - góc).
Từ trường hợp đồng dạng thứ hai, ta có thể suy ra một số hệ quả quan trọng:
Ví dụ 1: Cho tam giác ABC có MN // BC, AM = 2cm, MB = 3cm, AN = 2.5cm. Tính độ dài AC.
Giải:
Vì MN // BC nên ΔAMN ~ ΔABC. Do đó:
AM/AB = AN/AC
2/(2+3) = 2.5/AC
2/5 = 2.5/AC
AC = (2.5 * 5)/2 = 6.25cm
Ví dụ 2: Cho hình vẽ, biết AB = 6cm, AC = 8cm, AM = 3cm. Tính độ dài AN.
(Hình vẽ minh họa với MN // BC, ΔAMN ~ ΔABC)
Giải:
Vì MN // BC nên ΔAMN ~ ΔABC. Do đó:
AM/AB = AN/AC
3/6 = AN/8
AN = (3 * 8)/6 = 4cm
Để củng cố kiến thức về Trường hợp đồng dạng thứ hai của tam giác, bạn có thể thực hành giải các bài tập sau:
Lý thuyết Trường hợp đồng dạng thứ hai của tam giác là một công cụ quan trọng trong việc giải các bài toán liên quan đến tam giác đồng dạng. Việc hiểu rõ định nghĩa, điều kiện áp dụng và các hệ quả của trường hợp này sẽ giúp bạn tự tin hơn trong quá trình học tập và làm bài tập Toán 8.