Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 3 trang 57 sách giáo khoa Toán 8 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
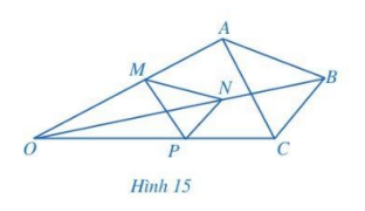
Trong Hình 15, cho
Đề bài
Trong Hình 15, cho \(MN\parallel AB,\,\,NP\parallel BC\). Chứng minh \(MP\parallel AC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào định lý Thales đảo để chứng minh \(MP\parallel AC\).
Lời giải chi tiết
Xét tam giác OAB có \(\frac{{OM}}{{MA}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Xét tam giác OBC có \(\frac{{OP}}{{PC}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Từ đó ta có \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}}\).
Xét tam giác OAC với \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}} \Rightarrow MP\parallel AC\) (Định lí Thales đảo).
Bài 3 trang 57 SGK Toán 8 – Cánh diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Bài 3 trang 57 thường yêu cầu học sinh chứng minh một hình là hình bình hành, hình chữ nhật, hình thoi hoặc hình vuông dựa trên các điều kiện cho trước. Phương pháp giải thường bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 3 trang 57. Giả sử bài toán yêu cầu chứng minh tứ giác ABCD là hình bình hành, với A(0;0), B(2;0), C(3;2), D(1;2).
Để chứng minh tứ giác ABCD là hình bình hành, ta cần chứng minh một trong các điều kiện sau:
Bước 1: Tính vector AB và CD
AB = (2-0; 0-0) = (2; 0)
CD = (1-3; 2-2) = (-2; 0)
Bước 2: So sánh vector AB và CD
Ta thấy AB = -CD, suy ra AB song song CD và AB = CD.
Kết luận: Tứ giác ABCD là hình bình hành.
Để củng cố kiến thức, bạn có thể giải các bài tập tương tự sau:
Cho hình bình hành ABCD. Gọi E là trung điểm của AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = 2FC.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 3 trang 57 SGK Toán 8 – Cánh diều. Chúc bạn học tập tốt!