Giaitoan.edu.vn xin giới thiệu bài giải chi tiết mục 2 trang 99 SGK Toán 8 tập 1 - Cánh diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 8 tập 1 - Cánh diều, đáp ứng nhu cầu học tập của học sinh.
Quan sát tứ giác ABCD ở Hình 16, đường chéo AC chia nó thành hai tam giác ABC và ACD. a) Gọi T1 và T2 lần lượt là tổng các góc của tam giác ABc và tam giác ACD. Tổng T1 + T2 bằng bao nhiêu độ? b) Gọi T là tổng các góc của tứ giác ABCD. So sánh T với T1 + T2.
Video hướng dẫn giải
Tìm x trong hình 18
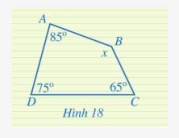
Phương pháp giải:
Áp dụng định lí tổng các góc của 1 tứ giác
Lời giải chi tiết:
Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)
Video hướng dẫn giải
Quan sát tứ giác ABCD ở Hình 16, đường chéo AC chia nó thành hai tam giác ABC và ACD.
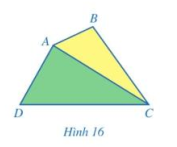
a) Gọi T1 và T2 lần lượt là tổng các góc của tam giác ABC và tam giác ACD. Tổng T1 + T2 bằng bao nhiêu độ?
b) Gọi T là tổng các góc của tứ giác ABCD. So sánh T với T1 + T2.
Phương pháp giải:
Áp dụng định lí tổng 3 góc trong 1 tam giác
Lời giải chi tiết:
a, \({T_1} = {180^0}\) (tổng 3 góc của \(\Delta ABC\))
\({T_2} = {180^0}\) (tổng 3 góc của \(\Delta ACD\))
\({T_1} + {T_2} = {180^0} + {180^0} = {360^0}\)
b,
\(\begin{array}{l}{T_6} = {360^0} \Rightarrow {T_6} = {T_1} + {T_2}\\{T_1} + {T_2} = {360^0}\end{array}\)
Video hướng dẫn giải
Quan sát tứ giác ABCD ở Hình 16, đường chéo AC chia nó thành hai tam giác ABC và ACD.

a) Gọi T1 và T2 lần lượt là tổng các góc của tam giác ABC và tam giác ACD. Tổng T1 + T2 bằng bao nhiêu độ?
b) Gọi T là tổng các góc của tứ giác ABCD. So sánh T với T1 + T2.
Phương pháp giải:
Áp dụng định lí tổng 3 góc trong 1 tam giác
Lời giải chi tiết:
a, \({T_1} = {180^0}\) (tổng 3 góc của \(\Delta ABC\))
\({T_2} = {180^0}\) (tổng 3 góc của \(\Delta ACD\))
\({T_1} + {T_2} = {180^0} + {180^0} = {360^0}\)
b,
\(\begin{array}{l}{T_6} = {360^0} \Rightarrow {T_6} = {T_1} + {T_2}\\{T_1} + {T_2} = {360^0}\end{array}\)
Video hướng dẫn giải
Tìm x trong hình 18
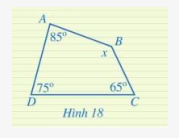
Phương pháp giải:
Áp dụng định lí tổng các góc của 1 tứ giác
Lời giải chi tiết:
Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)
Mục 2 trang 99 SGK Toán 8 tập 1 - Cánh diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Để giải quyết hiệu quả các bài toán trong mục này, học sinh cần nắm vững các khái niệm cơ bản về đa thức, phân thức đại số, và các phép toán liên quan.
Mục 2 trang 99 SGK Toán 8 tập 1 - Cánh diều thường bao gồm các dạng bài tập sau:
Để giải tốt các bài tập trong Mục 2 trang 99, học sinh cần:
Dưới đây là giải chi tiết các bài tập trong Mục 2 trang 99 SGK Toán 8 tập 1 - Cánh diều:
Cho đa thức A = 3x2 + 2xy - 5x2 + 4xy - x2. Hãy thu gọn đa thức A.
Giải:
A = (3x2 - 5x2 - x2) + (2xy + 4xy) = -3x2 + 6xy
Tìm bậc của đa thức B = 2x3y2 - 5x2y + 3xy2 - 7.
Giải:
Bậc của đa thức B là 5 (tổng số mũ của x và y trong mỗi hạng tử là 3+2=5, 2+1=3, 1+2=3, 0).
Cho hai đa thức P = x2 - 2xy + y2 và Q = x2 + 2xy + y2. Tính P + Q và P - Q.
Giải:
P + Q = (x2 - 2xy + y2) + (x2 + 2xy + y2) = 2x2 + 2y2
P - Q = (x2 - 2xy + y2) - (x2 + 2xy + y2) = -4xy
Xác định điều kiện xác định của phân thức M = \frac{x+1}{x-2}.
Giải:
Điều kiện xác định của phân thức M là x ≠ 2.
Rút gọn phân thức N = \frac{x^2 - 1}{x+1}.
Giải:
N = \frac{(x-1)(x+1)}{x+1} = x - 1 (với x ≠ -1)
Để học tốt môn Toán 8, học sinh nên:
Giaitoan.edu.vn hy vọng rằng bài giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về Mục 2 trang 99 SGK Toán 8 tập 1 - Cánh diều và đạt kết quả tốt trong học tập.