Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 113 và 114 sách giáo khoa Toán 8 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hình thoi ABCD có hai đường chéo là AC và BD cắt nhau tại O (hình 58) a) Hình thoi ABCD có là hình bình hành hay không? b) Hai đường chéo AC và BD có vuông góc với nhau hay không? c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của (widehat {BA{rm{D}}}) hay không?
Video hướng dẫn giải
Cho hình thoi ABCD có hai đường chéo là AC và BD cắt nhau tại O (hình 58)
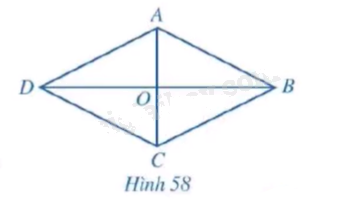
a) Hình thoi ABCD có là hình bình hành hay không?
b) Hai đường chéo AC và BD có vuông góc với nhau hay không?
c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay không?
Phương pháp giải:
Quan sát hình và chứng minh các tam giác tương ứng bằng nhau
Lời giải chi tiết:
a) Hình thoi ABCD có là hình bình hành (vì AB = BC = CD = DA)
b) Xét tam giác ABD có AB = AD nên tam giác ABD là tam giác cân tại A.
Suy ra đường trung tuyến AO đồng thời là đường cao.
Suy ra AO vuông góc với BD
Hay AC vuông góc với BD
c) Xét tam giác ABC và tam giác ADC có:
AD = AB
CD = CB
AC chung
\(\begin{array}{l}\Delta ABC = \Delta A{\rm{D}}C\\ \Rightarrow \widehat {DAC} = \widehat {BAC}\end{array}\)
Mà AC nằm giữa 2 tia AB và AD
Suy ra: AC là tia phân giác của góc BAD
Video hướng dẫn giải
Cho hình thoi ABCD có \(\widehat {ABC} = {120^o}\). Chứng minh tam giác ABD là tam giác đều.
Phương pháp giải:
Vận dụng các tính chất của hình thoi: chứng minh tam giác ABD cân tại A và có \(\widehat A = {60^o}\)
Lời giải chi tiết:
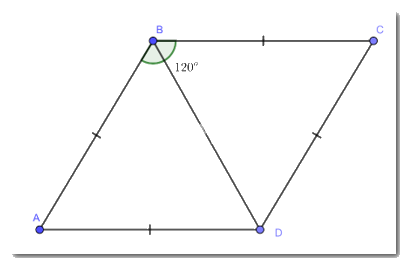
Vì ABCD là hình thoi
Suy ra: \(\widehat B = \widehat D = {120^o}\)
Mà: \(\widehat A = \widehat C\)
Mặt khác: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Suy ra: \(\widehat A = \widehat C = \dfrac{{{{360}^o} - \widehat B - \widehat D}}{2} = \dfrac{{{{360}^o} - {{120}^o} - {{120}^o}}}{2} = {60^o}\)
Xét tam giác ABD có AB = AD nên tam giác ABD là tam giác cân tại A mà \(\widehat A = {60^o}\)
Suy ra tam giác ABD là tam giác đều
Video hướng dẫn giải
Cho hình thoi ABCD có hai đường chéo là AC và BD cắt nhau tại O (hình 58)
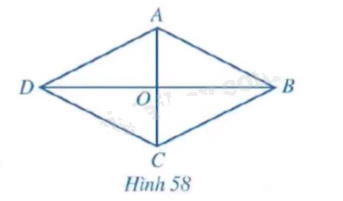
a) Hình thoi ABCD có là hình bình hành hay không?
b) Hai đường chéo AC và BD có vuông góc với nhau hay không?
c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay không?
Phương pháp giải:
Quan sát hình và chứng minh các tam giác tương ứng bằng nhau
Lời giải chi tiết:
a) Hình thoi ABCD có là hình bình hành (vì AB = BC = CD = DA)
b) Xét tam giác ABD có AB = AD nên tam giác ABD là tam giác cân tại A.
Suy ra đường trung tuyến AO đồng thời là đường cao.
Suy ra AO vuông góc với BD
Hay AC vuông góc với BD
c) Xét tam giác ABC và tam giác ADC có:
AD = AB
CD = CB
AC chung
\(\begin{array}{l}\Delta ABC = \Delta A{\rm{D}}C\\ \Rightarrow \widehat {DAC} = \widehat {BAC}\end{array}\)
Mà AC nằm giữa 2 tia AB và AD
Suy ra: AC là tia phân giác của góc BAD
Video hướng dẫn giải
Cho hình thoi ABCD có \(\widehat {ABC} = {120^o}\). Chứng minh tam giác ABD là tam giác đều.
Phương pháp giải:
Vận dụng các tính chất của hình thoi: chứng minh tam giác ABD cân tại A và có \(\widehat A = {60^o}\)
Lời giải chi tiết:
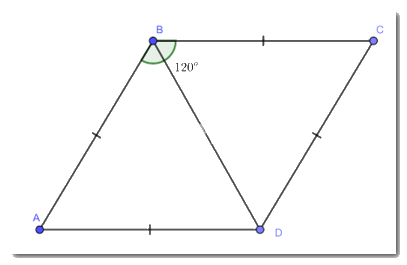
Vì ABCD là hình thoi
Suy ra: \(\widehat B = \widehat D = {120^o}\)
Mà: \(\widehat A = \widehat C\)
Mặt khác: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Suy ra: \(\widehat A = \widehat C = \dfrac{{{{360}^o} - \widehat B - \widehat D}}{2} = \dfrac{{{{360}^o} - {{120}^o} - {{120}^o}}}{2} = {60^o}\)
Xét tam giác ABD có AB = AD nên tam giác ABD là tam giác cân tại A mà \(\widehat A = {60^o}\)
Suy ra tam giác ABD là tam giác đều
Mục 2 của chương trình Toán 8 tập 1 - Cánh diều tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và kỹ năng tính toán.
Bài tập này yêu cầu học sinh thực hiện các phép toán cơ bản với đa thức như cộng, trừ, nhân, chia đa thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép toán với đa thức và thực hiện các phép tính một cách chính xác.
Bài tập này yêu cầu học sinh thực hiện các phép toán cơ bản với phân thức đại số như cộng, trừ, nhân, chia phân thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép toán với phân thức và thực hiện các phép tính một cách chính xác.
Bài tập này kết hợp các kiến thức về đa thức và phân thức đại số để giải quyết các bài toán phức tạp hơn. Để giải bài tập này, học sinh cần vận dụng linh hoạt các kiến thức đã học và tư duy logic để tìm ra lời giải.
Ví dụ: Rút gọn biểu thức: (x2 - 4) / (x + 2)
Khi giải bài tập về đa thức và phân thức đại số, học sinh cần chú ý đến các quy tắc về dấu, các phép toán cơ bản và các công thức rút gọn. Ngoài ra, học sinh cũng cần rèn luyện kỹ năng tư duy logic và kỹ năng giải quyết vấn đề để có thể giải quyết các bài toán phức tạp một cách hiệu quả.
Để giúp các em học sinh hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 113, 114 SGK Toán 8 tập 1 - Cánh diều, chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập. Các em có thể tham khảo lời giải này để tự học và rèn luyện kỹ năng giải toán.
Bài 1: (Giải chi tiết bài 1)...
Bài 2: (Giải chi tiết bài 2)...
Bài 3: (Giải chi tiết bài 3)...
Hy vọng rằng với những kiến thức và lời giải chi tiết mà chúng tôi đã cung cấp, các em học sinh sẽ có thể tự tin giải quyết các bài tập trong mục 2 trang 113, 114 SGK Toán 8 tập 1 - Cánh diều. Chúc các em học tập tốt!