Bài 2 trang 65 SGK Toán 8 – Cánh diều là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các phép biến đổi đại số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 65 SGK Toán 8 – Cánh diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB
Đề bài
Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho \(AP = PN = NB\). Gọi Q là giao điểm của AM và CP. Chừng minh:
a) \(MN//CP\)
b) \(AQ = QM\)
c) \(CP = 4PQ\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh MN là đường trung bình của tam giác BPC.
b) Sử dụng định lý Thales trong tam giác AMN để chứng minh.
c) Sử dụng định lý đường trung bình để chứng minh.
Lời giải chi tiết
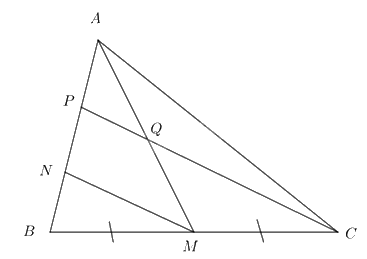
a) Vì \(AP = PN = NB\) nên N là trung điểm BP.
Mà M là trung điểm BC nên MN là đường trung bình của tam giác BPC.
\( \Rightarrow MN//CP\)
b) Tam giác AMN có \(MN//CP\) nên:
\(\frac{{AP}}{{PN}} = \frac{{AQ}}{{QM}}\) (Định lý Thales)
Mà \(AP = PN = NB\) nên P là trung điểm AN hay \(\frac{{AP}}{{PN}} = 1\)
\( \Rightarrow \frac{{AQ}}{{QM}} = 1 \Rightarrow AQ = QM\).
c) P là trung điểm AN, Q là trung điểm AM nên PQ là đường trung bình của tam giác AMN.
\( \Rightarrow PQ = \frac{1}{2}MN\)
Mà MN là đường trung bình của tam giác BPC nên \(MN = \frac{1}{2}CP \Rightarrow CP = 2MN\)
Vậy \(CP = 4PQ\).
Bài 2 trang 65 SGK Toán 8 – Cánh diều yêu cầu học sinh thực hiện các phép tính đại số, thường liên quan đến việc rút gọn biểu thức, giải phương trình hoặc chứng minh đẳng thức. Đề bài cụ thể sẽ khác nhau tùy theo từng phiên bản sách, nhưng thường tập trung vào việc vận dụng các quy tắc và tính chất đã học trong chương trình.
Để giải quyết hiệu quả các bài tập đại số như bài 2 trang 65 SGK Toán 8 – Cánh diều, học sinh cần nắm vững các phương pháp sau:
Để cung cấp lời giải chính xác, cần biết đề bài cụ thể của bài 2 trang 65. Tuy nhiên, dưới đây là một ví dụ minh họa cách giải một dạng bài tập thường gặp:
Đề bài: Rút gọn biểu thức: (2x + 3)(x - 1) - (x + 2)(2x - 1)
Lời giải:
Để tránh sai sót khi giải bài tập đại số, học sinh cần lưu ý những điều sau:
Các bài tập đại số không chỉ giúp học sinh rèn luyện kỹ năng tính toán mà còn có ứng dụng thực tế cao trong nhiều lĩnh vực khác nhau, như:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong SGK Toán 8 và các lớp học khác. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các phương pháp giải bài tập hiệu quả nhất. Hãy truy cập Giaitoan.edu.vn để học toán online ngay hôm nay!
| Công thức | Mô tả |
|---|---|
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |
| a2 - b2 = (a + b)(a - b) | Hiệu hai bình phương |