Chào mừng bạn đến với bài học lý thuyết Hằng đẳng thức đáng nhớ trong chương trình Toán 8 sách Cánh diều. Đây là một phần kiến thức nền tảng và vô cùng quan trọng, giúp bạn giải quyết nhiều bài toán đại số một cách nhanh chóng và hiệu quả.
Bài viết này sẽ cung cấp đầy đủ và chi tiết lý thuyết, các ví dụ minh họa, cùng với các bài tập vận dụng để bạn có thể nắm vững kiến thức này.
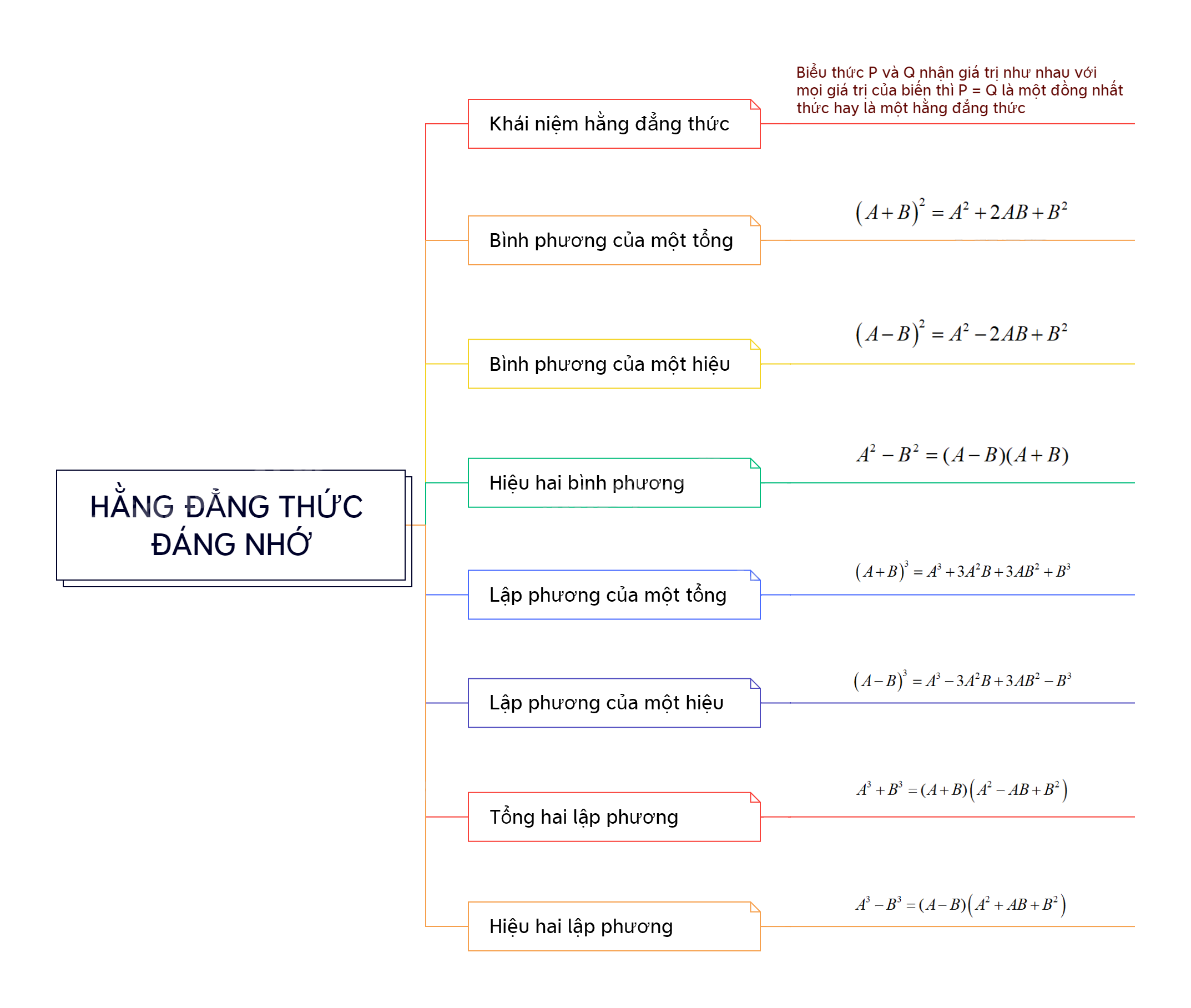
Hằng đẳng thức là gì?
Hằng đẳng thức
Nếu hai biểu thức P và Q nhận giá trị như nhau với mọi giá trị của biến thì ta nói P = Q là một đồng nhất thức hay là một hằng đẳng thức.
Ví dụ: \(a + b = b + a;a(a + 2) = {a^2} + 2a\) là những hằng đẳng thức.
\({a^2} - 1 = 3a;a(a - 1) = 2a\) không phải là những hằng đẳng thức.
1. Bình phương của một tổng là gì?
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Ví dụ: \({101^2} = {(100 + 1)^2} = {100^2} + 2.100.1 + {1^2} = 10201\)
2. Bình phương của một hiệu là gì?
\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Ví dụ: \({99^2} = {(100 - 1)^2} = {100^2} - 2.100.1 + {1^2} = 9801\)
3. Hiệu hai bình phương là gì?
\({A^2} - {B^2} = (A - B)(A + B)\)
Ví dụ: \({101^2} - {99^2} = (101 - 99)(101 + 99) = 2.200 = 400\)
4. Lập phương của một tổng là gì?
\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)
Ví dụ: \({\left( {x + 3} \right)^3} = {x^3} + 3{x^2}.3 + 3x{.3^2} + {3^3} = {x^3} + 9{x^2} + 27x + 27\)
5. Lập phương của một hiệu là gì?
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Ví dụ: \({\left( {x - 3} \right)^3} = {x^3} - 3{x^2}.3 + 3x{.3^2} - {3^3} = {x^3} - 9{x^2} + 27x - 27\)
6. Tổng hai lập phương là gì?
\({A^3} + {B^3} = (A + B)\left( {{A^2} - AB + {B^2}} \right)\)
Ví dụ: \({x^3} + 8 = {x^3} + {2^3} = (x + 2)({x^2} - 2x + 4)\)
7. Hiệu hai lập phương là gì?
\({A^3} - {B^3} = (A - B)\left( {{A^2} + AB + {B^2}} \right)\)
Ví dụ: \({x^3} - 8 = \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)\)
Hằng đẳng thức đáng nhớ là những đẳng thức luôn đúng với mọi giá trị của biến. Việc nắm vững các hằng đẳng thức này không chỉ giúp bạn giải toán nhanh hơn mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Dưới đây là các hằng đẳng thức đáng nhớ quan trọng nhất mà bạn cần nắm vững:
Ví dụ 1: Tính (x + 2)²
Áp dụng hằng đẳng thức (a + b)² = a² + 2ab + b², ta có:
(x + 2)² = x² + 2 * x * 2 + 2² = x² + 4x + 4
Ví dụ 2: Tính (3y - 1)²
Áp dụng hằng đẳng thức (a - b)² = a² - 2ab + b², ta có:
(3y - 1)² = (3y)² - 2 * 3y * 1 + 1² = 9y² - 6y + 1
Hãy tự giải các bài tập sau để kiểm tra mức độ hiểu bài của bạn:
Các hằng đẳng thức đáng nhớ không chỉ được sử dụng trong việc khai triển và phân tích đa thức mà còn có nhiều ứng dụng trong các bài toán khác như:
Khi áp dụng các hằng đẳng thức, bạn cần chú ý đến dấu của các số hạng. Ví dụ, (a - b)² khác với (a + b)².
Việc luyện tập thường xuyên sẽ giúp bạn nắm vững các hằng đẳng thức và áp dụng chúng một cách linh hoạt trong các bài toán.
| Hằng đẳng thức | Công thức |
|---|---|
| Bình phương của một tổng | (a + b)² = a² + 2ab + b² |
| Bình phương của một hiệu | (a - b)² = a² - 2ab + b² |
| Hiệu hai bình phương | a² - b² = (a + b)(a - b) |
| Lập phương của một tổng | (a + b)³ = a³ + 3a²b + 3ab² + b³ |
| Lập phương của một hiệu | (a - b)³ = a³ - 3a²b + 3ab² - b³ |
| Tổng hai lập phương | a³ + b³ = (a + b)(a² - ab + b²) |
| Hiệu hai lập phương | a³ - b³ = (a - b)(a² + ab + b²) |
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết Hằng đẳng thức đáng nhớ trong chương trình Toán 8 sách Cánh diều. Chúc bạn học tập tốt!