Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 2 trang 104, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán. Hãy cùng bắt đầu với bài 2 trang 104 nhé!
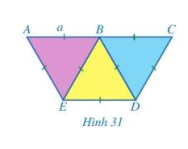
Người ta ghép ba hình tam giác đều
Đề bài
Người ta ghép ba hình tam giác đều với độ dài cạnh là a với vị trí như Hình 31.
a) Chứng minh ba điểm A, B, C thẳng hàng
b) Chứng minh tứ giác ACDE là hình thang cân.
c) Tính diện tích của tứ giác ACDE theo a.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Quan sát hình 3.
Lời giải chi tiết
a, Ta có: \(\widehat {ABE} + \widehat {EBD} + \widehat {DBC} = 60^0 + 60^0 + 60^0 = {180^0}\)
Suy ra 3 điểm A, B, C thẳng hàng
b, Do:
\(\begin{array}{l}\widehat {BDE} = \widehat {DBC} = {60^0} \Rightarrow ED//BC\left( 1 \right)\\\widehat {BED} = \widehat {EBA} = {60^0} \Rightarrow ED//AB\left( 2 \right)\end{array}\)
Từ (1), (2) suy ra: ED//AC suy ra tứ giác ACDE là hình thang
Mà: \(\widehat {EAC} = \widehat {DCA} = {60^0}\) suy ra hình thang ACDE là hình thang cân
c, Gọi BH là đường cao của tam giác BDE. Áp dụng định lí Pythagore vào tam giác BHD vuông tại H, ta có:
\(B{D^2} = B{H^2} + H{D^2} \Rightarrow B{H^2} = B{D^2} - H{D^2} = {a^2} - \frac{{{a^2}}}{4} = a\sqrt {\frac{3}{4}} \)
AC = a + a = 2a
Diện tích của tứ giác ACDE là: \({S_{ABCD}} = \frac{1}{2}.BH.(ED + AC) = \frac{1}{2}.a\sqrt {\frac{3}{4}} .(2a + a) = \frac{{3{a^2}}}{2}\sqrt {\frac{3}{4}} \)
Bài 2 trang 104 SGK Toán 8 tập 1 - Cánh diều thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Bài 2 trang 104 SGK Toán 8 tập 1 - Cánh diều thường yêu cầu học sinh chứng minh một tứ giác là hình thang cân, hoặc tính toán các yếu tố liên quan đến hình thang cân như độ dài cạnh, góc, đường chéo. Để giải bài tập này, chúng ta cần:
Đề bài: Cho hình thang ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Chứng minh rằng MN // AB // CD.
Giải:
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập sau:
Để học Toán 8 hiệu quả, bạn nên:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 2 trang 104 SGK Toán 8 tập 1 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!