Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 84 SGK Toán 8 Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 8.
Bài giải này được xây dựng dựa trên chương trình học Toán 8 Cánh diều, đảm bảo tính chính xác và phù hợp với nội dung sách giáo khoa.
Cho hai tam giác ABC và A’B’C’ có
Video hướng dẫn giải
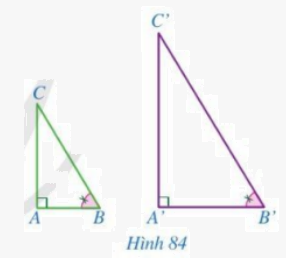
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\widehat {B'} = \widehat B\) (Hình 84). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\).
Phương pháp giải:
Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ ba.
Lời giải chi tiết:
Xét tam giác A’B’C’ và tam giác ABC có:
\(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (g-g)
Video hướng dẫn giải
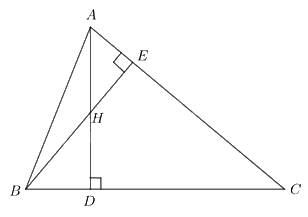
Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh \(HA.HD = HB.HE\).
Phương pháp giải:
- Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác EHA và DHB đồng dạng.
- Suy ra tỉ số đồng dạng tương ứng.
Lời giải chi tiết:
Xét tam giác EHA và tam giác DHB có:
\(\widehat {EHA} = \widehat {DHB}\) (đối đỉnh)
\(\widehat {AEH} = \widehat {BDH} = 90^\circ \)
\( \Rightarrow \Delta EHA \backsim \Delta DHB\) (g-g)
\( \Rightarrow \frac{{HA}}{{HB}} = \frac{{HE}}{{HD}}\) (Tỉ số đồng dạng)
\( \Rightarrow HA.HD = HB.HE\)
Video hướng dẫn giải
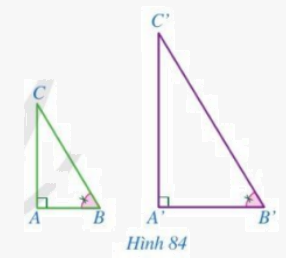
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\widehat {B'} = \widehat B\) (Hình 84). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\).
Phương pháp giải:
Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ ba.
Lời giải chi tiết:
Xét tam giác A’B’C’ và tam giác ABC có:
\(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (g-g)
Video hướng dẫn giải
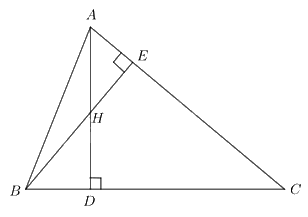
Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh \(HA.HD = HB.HE\).
Phương pháp giải:
- Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác EHA và DHB đồng dạng.
- Suy ra tỉ số đồng dạng tương ứng.
Lời giải chi tiết:
Xét tam giác EHA và tam giác DHB có:
\(\widehat {EHA} = \widehat {DHB}\) (đối đỉnh)
\(\widehat {AEH} = \widehat {BDH} = 90^\circ \)
\( \Rightarrow \Delta EHA \backsim \Delta DHB\) (g-g)
\( \Rightarrow \frac{{HA}}{{HB}} = \frac{{HE}}{{HD}}\) (Tỉ số đồng dạng)
\( \Rightarrow HA.HD = HB.HE\)
Mục 2 trang 84 SGK Toán 8 – Cánh diều tập trung vào việc vận dụng các kiến thức đã học về hình hộp chữ nhật và hình lập phương để giải các bài toán thực tế. Các bài tập thường yêu cầu tính diện tích xung quanh, diện tích toàn phần, thể tích của các hình này. Để giải quyết hiệu quả, học sinh cần nắm vững các công thức và hiểu rõ mối liên hệ giữa các yếu tố hình học.
Mục 2 bao gồm một số bài tập với mức độ khó tăng dần. Các bài tập đầu tiên thường là những bài tập cơ bản, giúp học sinh ôn lại kiến thức về công thức tính diện tích và thể tích. Các bài tập sau sẽ phức tạp hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học và có khả năng phân tích, suy luận logic.
Bài tập này yêu cầu học sinh tính diện tích xung quanh của một hình hộp chữ nhật cho trước. Để giải bài này, học sinh cần xác định đúng chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật, sau đó áp dụng công thức tính diện tích xung quanh: 2(dài + rộng) x cao.
Bài tập này yêu cầu học sinh tính diện tích toàn phần của một hình hộp chữ nhật cho trước. Để giải bài này, học sinh cần tính diện tích xung quanh và diện tích hai đáy của hình hộp chữ nhật, sau đó cộng lại. Công thức tính diện tích toàn phần: Diện tích xung quanh + 2 x (dài x rộng).
Bài tập này yêu cầu học sinh tính thể tích của một hình hộp chữ nhật cho trước. Để giải bài này, học sinh cần xác định đúng chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật, sau đó áp dụng công thức tính thể tích: dài x rộng x cao.
Bài tập này thường đưa ra một tình huống thực tế, yêu cầu học sinh vận dụng kiến thức về diện tích và thể tích để giải quyết. Ví dụ, tính lượng sơn cần thiết để sơn một căn phòng, tính lượng nước cần thiết để đổ đầy một bể nước, v.v.
Bài toán: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.
Giải:
Việc giải các bài tập trong Mục 2 trang 84 SGK Toán 8 – Cánh diều đòi hỏi học sinh phải nắm vững kiến thức cơ bản và có khả năng vận dụng linh hoạt các công thức. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em sẽ tự tin giải quyết các bài tập Toán 8 một cách dễ dàng và đạt kết quả tốt nhất.