Bài học về Lý thuyết Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản là một phần quan trọng của chương trình Toán 8 - Cánh Diều. Nó giúp học sinh làm quen với những khái niệm cơ bản về xác suất, một lĩnh vực ứng dụng rộng rãi trong đời sống.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập liên quan.
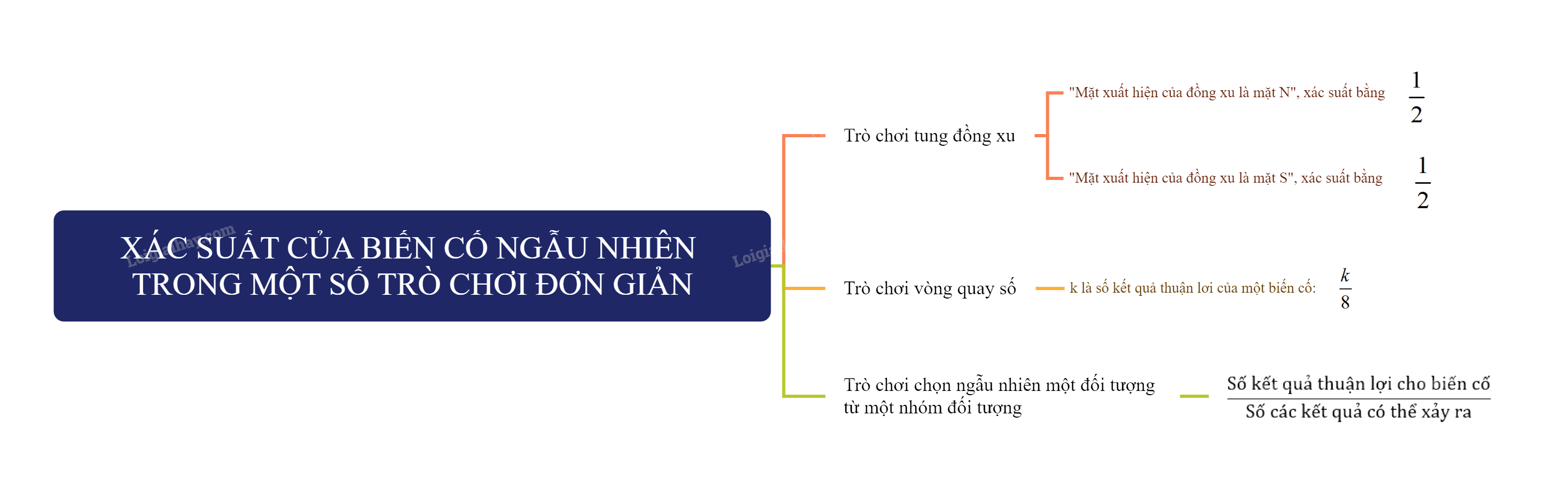
Cách tính xác suất của biến cố ngẫu nhiên
1. Xác suất của biến cố trong trò chơi tung đồng xu
Trong trò chơi tung đồng xu, ta có:
- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt N” bằng \(\frac{1}{2}\).
- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt S” bằng \(\frac{1}{2}\).
2. Xác suất của biến cố trong trò chơi vòng quay số
Trong trò chơi vòng quay số đã nêu, nếu k là số kết quả thuận lợi cho một biến cố thì xác suất của biến cố đó bằng \(\frac{k}{8}\).
3. Xác suất của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng
Trong trò chơi ngẫu nhiên, một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.
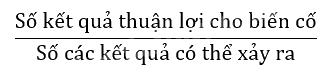
Xác suất là một khái niệm toán học dùng để đo lường khả năng xảy ra của một sự kiện. Trong cuộc sống hàng ngày, chúng ta thường gặp những tình huống không chắc chắn, và xác suất giúp chúng ta đưa ra những dự đoán có căn cứ hơn. Bài học này sẽ giới thiệu cho học sinh lớp 8 về lý thuyết xác suất thông qua các trò chơi đơn giản, giúp các em hiểu rõ hơn về khái niệm này.
Một biến cố ngẫu nhiên là một sự kiện mà kết quả của nó không thể đoán trước một cách chắc chắn. Ví dụ, khi tung một đồng xu, kết quả có thể là mặt ngửa hoặc mặt sấp. Mỗi kết quả này là một biến cố ngẫu nhiên.
Xác suất của một biến cố A, ký hiệu là P(A), là một số thực nằm trong khoảng từ 0 đến 1. Nó cho biết mức độ khả năng xảy ra của biến cố A.
Công thức tính xác suất:
P(A) = (Số kết quả thuận lợi cho A) / (Tổng số kết quả có thể xảy ra)
Ví dụ 1: Tung đồng xu
Xác suất để đồng xu xuất hiện mặt ngửa là:
P(Ngửa) = 1 / 2 = 0.5
Ví dụ 2: Gieo xúc xắc 6 mặt
Xác suất để gieo được mặt 3 là:
P(3) = 1 / 6
Ví dụ 3: Rút một lá bài từ bộ bài 52 lá
Xác suất để rút được lá Át là:
P(Át) = 4 / 52 = 1 / 13
Bài 1: Một hộp có 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên một quả bóng. Tính xác suất để lấy được quả bóng đỏ.
Bài 2: Gieo một con xúc xắc 6 mặt. Tính xác suất để gieo được một số chẵn.
Bài 3: Trong một lớp học có 20 học sinh, có 12 học sinh thích môn Toán và 8 học sinh thích môn Văn. Chọn ngẫu nhiên một học sinh. Tính xác suất để học sinh đó thích môn Toán.
Lý thuyết xác suất không chỉ dừng lại ở những trò chơi đơn giản. Nó còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như:
Bài học về Lý thuyết Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản là nền tảng quan trọng để học sinh hiểu rõ hơn về khái niệm xác suất và ứng dụng của nó trong thực tế. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán liên quan một cách dễ dàng và tự tin hơn.
Hy vọng rằng, với những kiến thức và ví dụ minh họa trên, các em học sinh lớp 8 - Cánh Diều đã có thể hiểu rõ hơn về Lý thuyết Xác suất. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và nâng cao kỹ năng giải toán nhé!