Giải bài 15 trang 30 SBT Toán 10 - Cánh Diều

Giải bài 15 trang 30 SBT toán 10 - Cánh diều

Giải bài 15 trang 30 SBT Toán 10 - Cánh Diều

Bài 15 trang 30 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, giúp củng cố và nâng cao hiểu biết về vectơ.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 15 trang 30 SBT Toán 10 Cánh Diều, giúp các em học sinh tự tin hơn trong quá trình học tập và ôn luyện.

Biểu diễn miền nghiệm của hệ bất phương trình:

Đề bài

Biểu diễn miền nghiệm của hệ bất phương trình:

a) \(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 3}\\{x + y \ge - 3}\end{array}} \right.\) b) \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 5}\\{x - 2y \le 2}\\{x \ge - 1}\end{array}} \right.\) c) \(\left\{ {\begin{array}{*{20}{c}}{ - 3x + 2y < 6}\\{x - 2y \ge - 2}\\{2x + y < 4}\end{array}} \right.\)

Phương pháp giải - Xem chi tiết Giải bài 15 trang 30 SBT toán 10 - Cánh diều 1

Bước 1: Vẽ đường thẳng \(d:x - 2y = 4\).
Bước 2: Lấy một điểm \(M\left( {{x_o};{y_o}} \right)\) không nằm trên d (ta thường lấy gốc tọa độ O nếu \(c \ne 0\). Tính \(a{x_o} + b{y_o}\) và so sánh với c
Bước 3: Kết luận
- Nếu \(a{x_o} + b{y_o} < c\)thì nửa mặt phẳng (không kể đường thẳng d) chứa điểm M là miền nghiệm của bất phương trình \(ax + by < c\)
- Nếu \(a{x_o} + b{y_o} > c\) thì nửa mặt phẳng (không kể d) không chứa điểm M là miền nghiệm của bất phương trình \(ax + by > c\)

Lời giải chi tiết

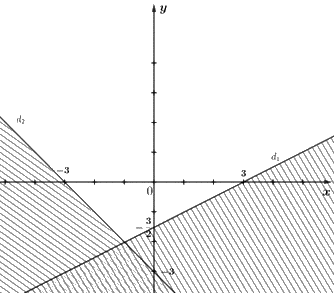
a) Ta có hai đường thẳng: \({d_1}:x - 2y = 3;{d_2}:x + y = - 3\)

+) Lấy O(0; 0) không thuộc vào đường thẳng d₁ có 0 – 2.0 = 0 < 3. Do đó miền nghiệm của bất phương trình x – 2y ≤ 3 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.

+) Lấy O(0; 0) không thuộc đường thẳng d₂ có 0 + 0 = 0 > – 3. Do đó miền nghiệm của bất phương trình x + y ≥ – 3 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₂.

Miền nghiệm của hệ bất phương trình là miền không bị gạch như trong hình vẽ sau:

Giải bài 15 trang 30 SBT toán 10 - Cánh diều 2

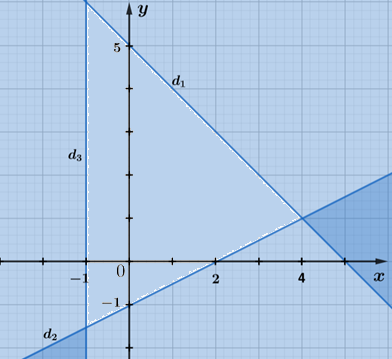
b) Ta có b đường thẳng: \({d_1}:x + y = 5;{d_2}:x - 2y = 2;{d_3}:x = - 1\)

+) Lấy O(0; 0) không thuộc đường thẳng d₁ có 0 + 0 = 0 < 5. Do đó miền nghiệm của bất phương trình x + y ≤ 5 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.

+) Lấy O(0; 0) không thuộc đường thẳng d₂ có 0 – 2.0 = 0 < 2. Do đó miền nghiệm của bất phương trình x – 2y ≤ 2 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₂.

+) Lấy O(0; 0) không thuộc đường thẳng d₃ có 0 ≥ – 1. Do đó miền nghiệm của bất phương trình x ≥ – 1 là nửa mặt phẳng chứa điểm O(0; 0) và có bờ là đường thẳng d₃.

Miền nghiệm của hệ bất phương trình được biểu diễn là miền màu trắng trong hình vẽ sau:

Giải bài 15 trang 30 SBT toán 10 - Cánh diều 3

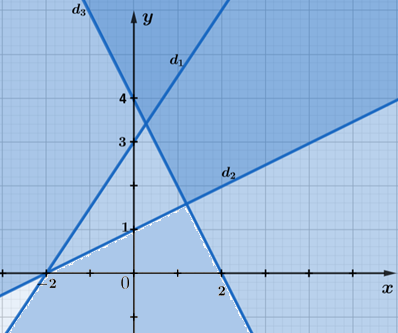
c) Ta có ba đường thẳng: \({d_1}: - 3x + 2y = 6;{d_2}:x - 2y = - 2;{d_3}:2x + y = 4\)

+) Lấy O(0; 0) không thuộc đường thẳng d₁ có – 3.0 + 2.0 = 0 < 6. Do đó miền nghiệm của bất phương trình – 3x + 2y < 6 là nửa mặt phẳng chứa điểm O(0; 0) không kể bờ là đường thẳng d₁.

+) Lấy O(0; 0) không thuộc đường thẳng d₂ có 0 – 2.0 = 0 > – 2 . Do đó miền nghiệm của bất phương trình x – 2y ≥ – 2 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₂.

+) Lấy O(0; 0) không thuộc đường thẳng d₃ có 2.0 + 0 < 4. Do đó miền nghiệm của bất phương trình 2x + y < 4 là nửa mặt phẳng chứa điểm O(0; 0) và không kể bờ là đường thẳng d₃.

Miền nghiệm của hệ bất phương trình được biểu diễn là miền không tô màu như trong hình vẽ sau:

Giải bài 15 trang 30 SBT toán 10 - Cánh diều 4

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 15 trang 30 SBT toán 10 - Cánh diều đặc sắc thuộc chuyên mục toán lớp 10 trên nền tảng toán học. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 15 trang 30 SBT Toán 10 - Cánh Diều: Tổng quan và Phương pháp giải

Bài 15 trang 30 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:

Định nghĩa vectơ: Vectơ là một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối.
Các phép toán vectơ: Cộng, trừ, nhân với một số thực.
Tích vô hướng của hai vectơ: Công thức tính tích vô hướng và ứng dụng để xác định góc giữa hai vectơ, tính độ dài vectơ.
Hệ tọa độ: Biểu diễn vectơ trong hệ tọa độ và thực hiện các phép toán vectơ trong hệ tọa độ.

Nội dung chi tiết bài 15 trang 30 SBT Toán 10 - Cánh Diều

Bài 15 thường bao gồm các dạng bài tập sau:

Bài tập về tìm tọa độ của vectơ: Cho các điểm trong không gian, tìm tọa độ của vectơ tạo bởi các điểm đó.
Bài tập về thực hiện các phép toán vectơ: Tính tổng, hiệu, tích với một số thực của các vectơ.
Bài tập về tích vô hướng: Tính tích vô hướng của hai vectơ, xác định góc giữa hai vectơ.
Bài tập ứng dụng: Giải các bài toán liên quan đến hình học sử dụng vectơ.

Lời giải chi tiết bài 15 trang 30 SBT Toán 10 - Cánh Diều

Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 15 trang 30 SBT Toán 10 Cánh Diều. (Ở đây sẽ là nội dung giải chi tiết từng câu hỏi của bài 15, ví dụ:)

Ví dụ: Giải câu a bài 15 trang 30 SBT Toán 10 - Cánh Diều

(Nội dung câu a của bài 15)

Lời giải:

(Giải thích chi tiết từng bước giải câu a, kèm theo công thức và lý thuyết liên quan)

Ví dụ: Giải câu b bài 15 trang 30 SBT Toán 10 - Cánh Diều

(Nội dung câu b của bài 15)

Lời giải:

(Giải thích chi tiết từng bước giải câu b, kèm theo công thức và lý thuyết liên quan)

Mẹo giải nhanh bài tập về vectơ

Để giải nhanh các bài tập về vectơ, các em có thể áp dụng một số mẹo sau:

Sử dụng công thức: Nắm vững các công thức về vectơ và áp dụng một cách linh hoạt.
Vẽ hình: Vẽ hình minh họa giúp các em hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
Biến đổi vectơ: Sử dụng các phép biến đổi vectơ để đơn giản hóa bài toán.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự và luyện tập thêm

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, các em có thể tham khảo thêm các bài tập tương tự trong SBT Toán 10 Cánh Diều và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.

Kết luận

Bài 15 trang 30 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh nắm vững kiến thức về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và các mẹo giải nhanh mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và ôn luyện môn Toán.