Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 56 trang 17 trong sách bài tập (SBT) Toán 10 - Cánh Diều.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn hiểu rõ các khái niệm Toán học một cách hiệu quả.
Trong kì thi chọn học sinh giỏi các môn văn hóa, lớp 10A có 7 học sinh đăng kí thi môn Toán, 5 học sinh đăng kí thi môn Vật lí, 6 học sinh đăng kí thi môn Hóa học; trong đó có 3 học sinh đăng kí thi cả Toán và Vật lí, 4 học sinh đăng kí thi cả Toán và Hóa học, 2 học sinh đăng kí thi cả Vật lí và Hóa học, 1 học sinh đăng kí thi cả ba môn. Hỏi lớp 10A có tất cả bao nhiêu học sinh đăng kí thi học sinh giỏi các môn Toán, Vật lí, Hóa học?
Đề bài
Trong kì thi chọn học sinh giỏi các môn văn hóa, lớp 10A có 7 học sinh đăng kí thi môn Toán, 5 học sinh đăng kí thi môn Vật lí, 6 học sinh đăng kí thi môn Hóa học; trong đó có 3 học sinh đăng kí thi cả Toán và Vật lí, 4 học sinh đăng kí thi cả Toán và Hóa học, 2 học sinh đăng kí thi cả Vật lí và Hóa học, 1 học sinh đăng kí thi cả ba môn. Hỏi lớp 10A có tất cả bao nhiêu học sinh đăng kí thi học sinh giỏi các môn Toán, Vật lí, Hóa học?
Phương pháp giải - Xem chi tiết
Sử dụng biểu đồ Ven.
Lời giải chi tiết
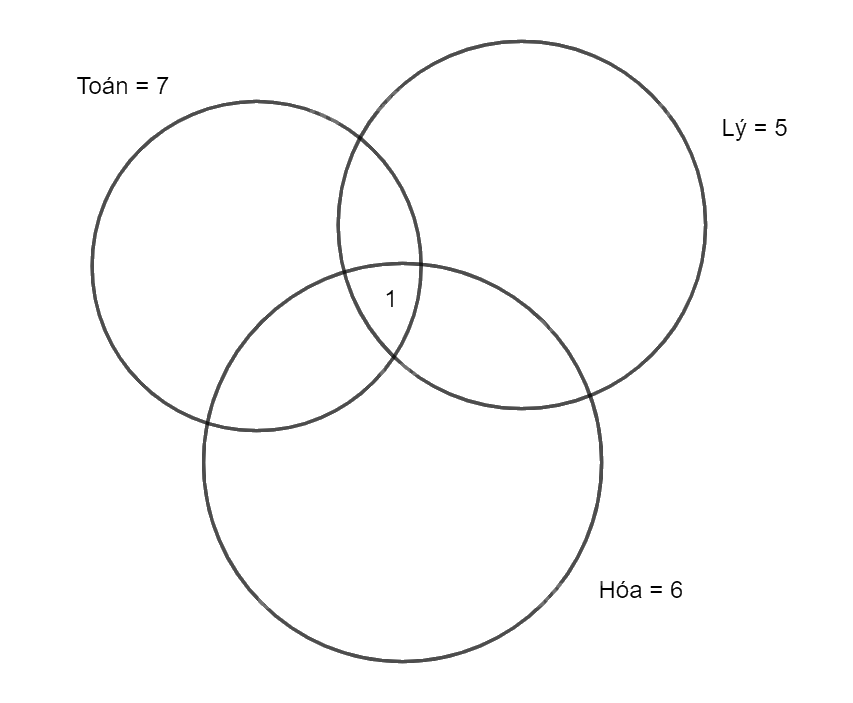
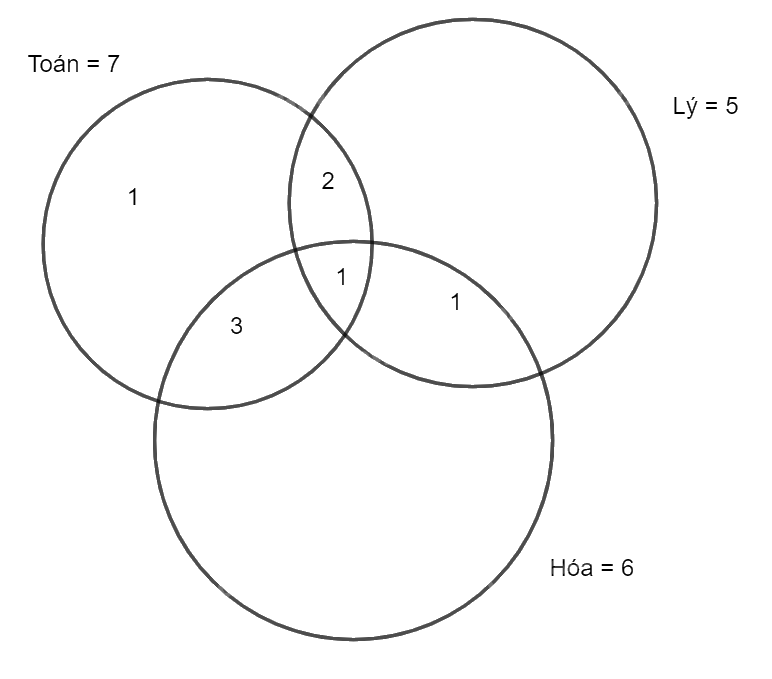
Số học sinh thi môn Toán là 7, Lý là 5, Hóa là 6. Tương ứng với ba vòng tròn.
Số học sinh đăng kí thi ba môn là 1 nên phần giao của ba môn là 1.
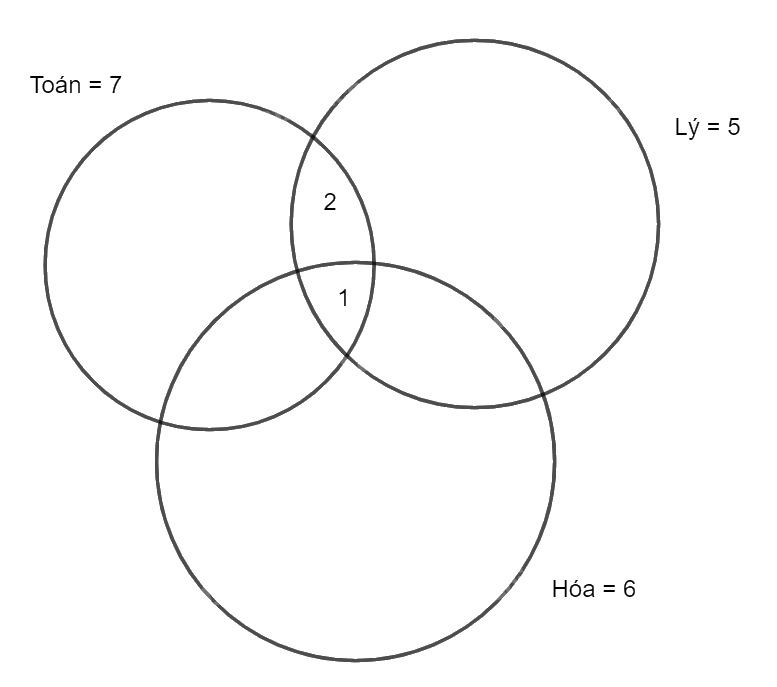
Số học sinh đăng kí thi Toán và Lý là 3 nên tổng phần giao của Toán, Lý là 3, trừ đi phần giao của ba môn là 1, còn 2 chỉ thi Toán, Lý.
Số học sinh đăng kí thi Toán và Hóa là 4 nên tổng phần giao của Toán, Hóa là 4, trừ đi phần giao của ba môn là 1, còn 3 chỉ thi Toán, Hóa.
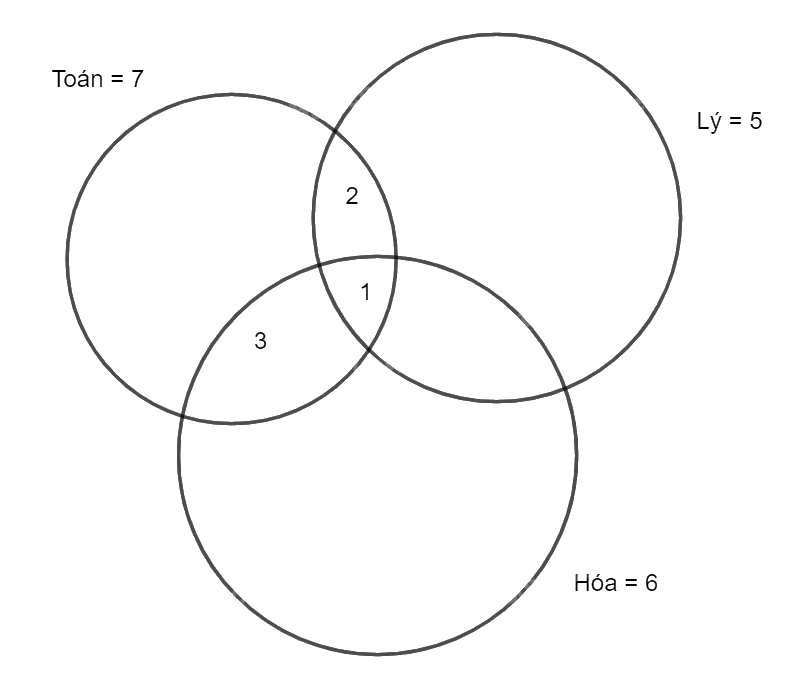
Số học sinh đăng kí thi Lý và Hóa là 2 nên tổng phần giao của Lý, Hóa là 2, trừ đi phần giao của ba môn là 1, còn 1 chỉ thi Lý, Hóa.
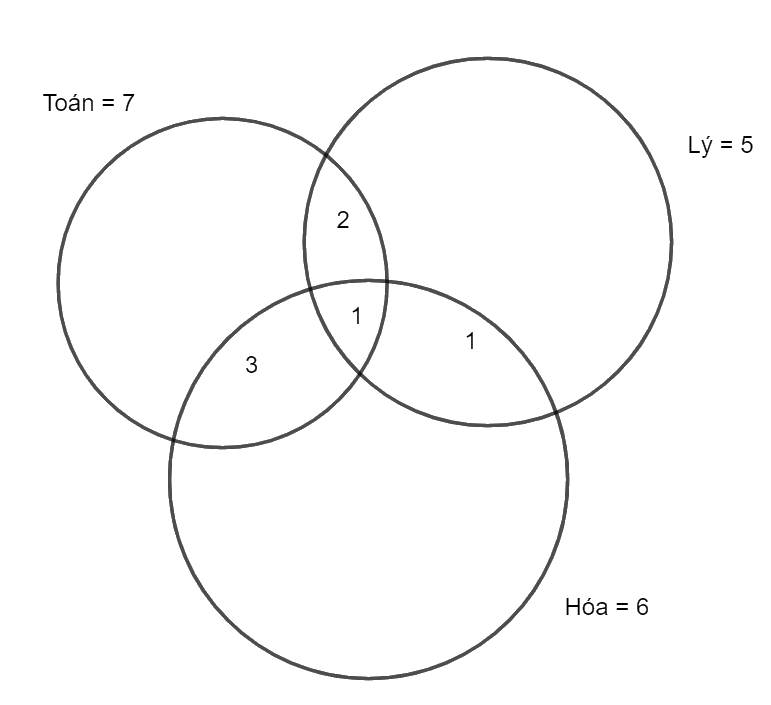
Phần còn lại của vòng tròn Toán (chỉ thi Toán) là 7 – 2 – 1 – 3 = 1.
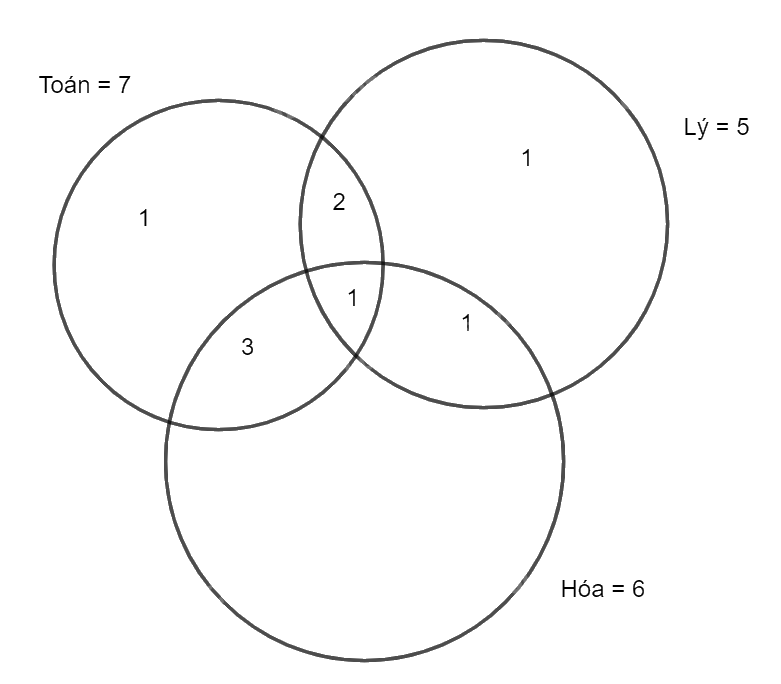
Phần còn lại của vòng tròn Lý (chỉ thi Lý) là 5 – 2 – 1 – 1 = 1.
Phần còn lại của vòng tròn Hóa (chỉ thi Hóa) là 6 – 3 – 1 – 1 = 1.
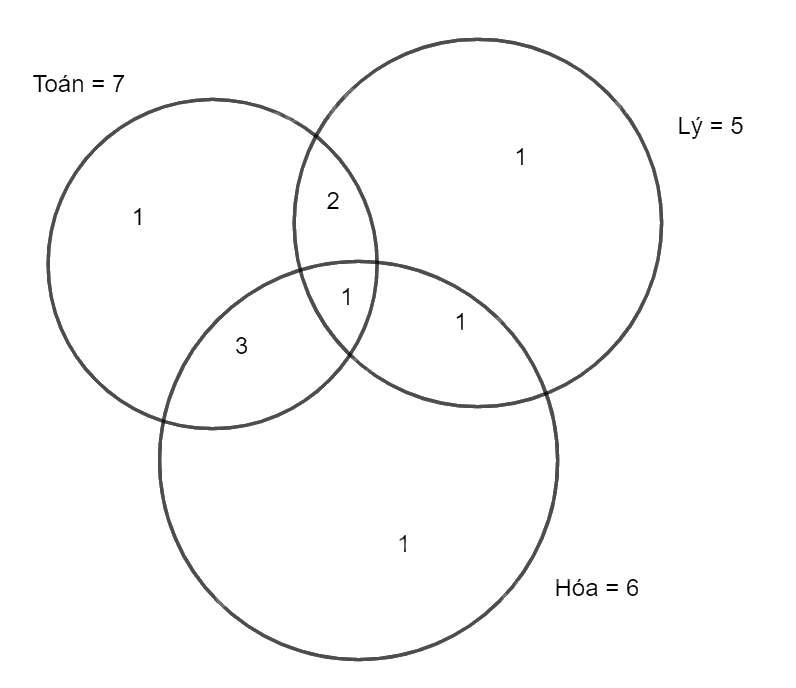
Vậy để tính tổng số học sinh đăng kí dự thi, ta cộng tổng tất cả các phần:
1 + 2 + 1 + 3 + 1 + 1 + 1 = 10 (học sinh).
Bài 56 trang 17 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ, và các ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh phải hiểu rõ định nghĩa vectơ, các phép cộng, trừ, nhân vectơ với một số thực, và cách biểu diễn vectơ trong hệ tọa độ.
Bài 56 thường bao gồm các dạng bài tập sau:
Để giải bài 56 trang 17 SBT Toán 10 - Cánh Diều một cách hiệu quả, bạn cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 56 (giả sử bài 56 có nhiều câu hỏi):
Đề bài: (Ví dụ) Cho \vec{a} = (1; 2)" và \vec{b} = (-3; 4)". Tính \vec{a} + \vec{b}".
Lời giải:
\vec{a} + \vec{b} = (1 + (-3); 2 + 4) = (-2; 6)"
Đề bài: (Ví dụ) Chứng minh rằng nếu \vec{AB} = \vec{CD}" thì tứ giác ABCD là hình bình hành.
Lời giải:
Nếu \vec{AB} = \vec{CD}" thì AB song song với CD và AB = CD. Do đó, tứ giác ABCD là hình bình hành.
Để giải các bài tập về vectơ một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức về vectơ, bạn có thể làm thêm các bài tập tương tự sau:
Bài 56 trang 17 SBT Toán 10 - Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng vận dụng kiến thức về vectơ vào giải quyết các bài toán thực tế. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ có thể giải bài tập này một cách dễ dàng và hiệu quả.