Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 10 Cánh diều. Bài viết này sẽ hướng dẫn bạn giải bài 58 trang 90 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin hơn trong việc chinh phục môn Toán.
Trong mặt phẳng toạ độ Oxy, cho điểm M(1 ; 1) và đường thẳng ∆: 3x + 4y + 3 = 0. Viết phương trình đường tròn (C), biết (C) có tâm M và đường thẳng ∆ cắt (C) tại hai điểm N, P thoả mãn tam giác MNP đều.
Đề bài
Trong mặt phẳng toạ độ Oxy, cho điểm M(1 ; 1) và đường thẳng : 3x + 4y + 3 = 0. Viết phương trình đường tròn (C), biết (C) có tâm M và đường thẳng∆ cắt (C) tại hai điểm N, P thoả mãn tam giác MNP đều.
Phương pháp giải - Xem chi tiết
Tìm bán kính đường tròn (C)
Bước 1: Tính khoảng cách từ M đến ∆
Bước 2: Xét ∆MNP đều biết độ dài đường cao kẻ từ M, tính độ dài các cạnh của tam giác là bán kính của (C)
Bước 3: Viết PT đường tròn với tâm M và bán kính tìm được ở bước 2
Lời giải chi tiết
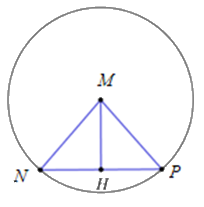
Gọi H là hình chiếu của M lên đường thẳng ∆
Ta có: \(MH = d(M,\Delta ) = \frac{{\left| {3 + 4 + 3} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 2\)
Theo giả thiết, ∆MNP đều \( \Rightarrow \widehat {MNH} = {60^0}\)
Xét \(\Delta MNH\) vuông tại H có \(MN = \frac{{MH}}{{\sin \widehat {MNH}}} = \frac{2}{{\sin {{60}^0}}} = \frac{{4\sqrt 3 }}{3}\)\( \Rightarrow R = \frac{{4\sqrt 3 }}{3}\)
Vậy (C) có PT: \({(x - 1)^2} + {(y - 1)^2} = \frac{{16}}{3}\)
Bài 58 trang 90 SBT Toán 10 Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong hình học. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 58 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng bài tập trong bài 58. (Lưu ý: Vì bài tập cụ thể không được cung cấp, phần này sẽ trình bày cách tiếp cận chung và ví dụ minh họa)
Đề bài: Cho hai vectơ a = (2; -1) và b = (-3; 4). Tính a.b.
Lời giải:
Tích vô hướng của hai vectơ a = (x1; y1) và b = (x2; y2) được tính theo công thức:
a.b = x1x2 + y1y2
Áp dụng công thức vào bài toán, ta có:
a.b = 2*(-3) + (-1)*4 = -6 - 4 = -10
Vậy, a.b = -10.
Đề bài: Cho hai vectơ a = (1; 0) và b = (1; 1). Tính góc θ giữa hai vectơ.
Lời giải:
Công thức tính góc θ giữa hai vectơ a và b là:
cos θ = (a.b) / (||a|| * ||b||)
Trong đó, ||a|| là độ dài của vectơ a, được tính bằng công thức:
||a|| = √(x12 + y12)
Tính toán:
cos θ = 1 / (1 * √2) = 1/√2
θ = 45°
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 58 trang 90 SBT Toán 10 Cánh Diều. Hãy luyện tập thêm các bài tập tương tự để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc bạn học tốt!